Free Statistics
of Irreproducible Research!
Description of Statistical Computation | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Author's title | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Author | *The author of this computation has been verified* | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| R Software Module | rwasp_linear_regression.wasp | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
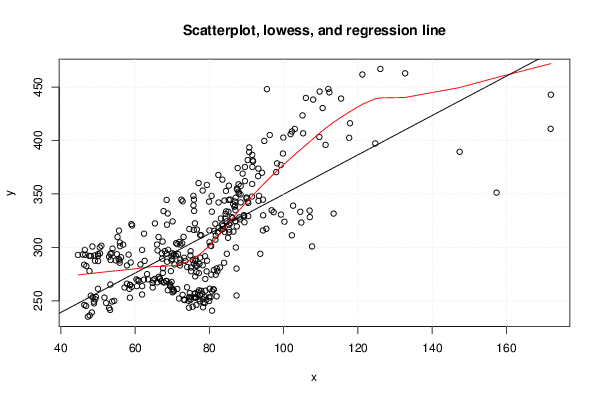
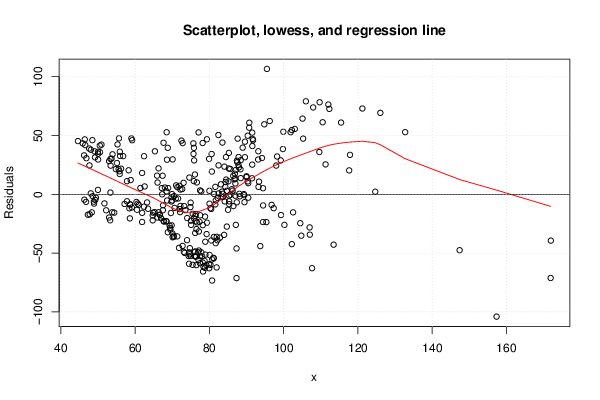
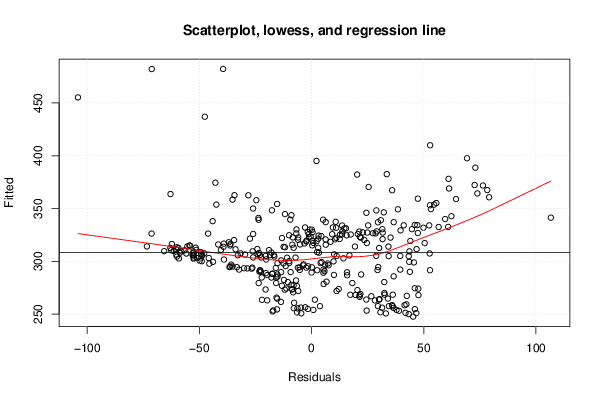
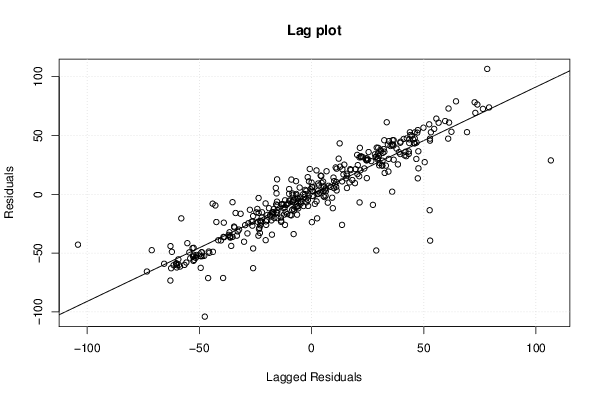
| Title produced by software | Linear Regression Graphical Model Validation | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Date of computation | Tue, 11 Dec 2012 10:09:14 -0500 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Cite this page as follows | Statistical Computations at FreeStatistics.org, Office for Research Development and Education, URL https://freestatistics.org/blog/index.php?v=date/2012/Dec/11/t1355238566ipugm7g8vxjt4co.htm/, Retrieved Tue, 18 Feb 2025 22:21:27 +0000 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Statistical Computations at FreeStatistics.org, Office for Research Development and Education, URL https://freestatistics.org/blog/index.php?pk=198527, Retrieved Tue, 18 Feb 2025 22:21:27 +0000 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| QR Codes: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Original text written by user: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| IsPrivate? | No (this computation is public) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| User-defined keywords | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Estimated Impact | 172 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Tree of Dependent Computations | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Family? (F = Feedback message, R = changed R code, M = changed R Module, P = changed Parameters, D = changed Data) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| - [Linear Regression Graphical Model Validation] [] [2011-11-17 10:24:03] [a2638725f7f7c6bd63902ba17eba666b] - R [Linear Regression Graphical Model Validation] [wspap] [2012-12-11 15:09:14] [fa3197be492c9e61892dda11815d51ad] [Current] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Feedback Forum | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Post a new message | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Dataset | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Dataseries X: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
87.28 87.28 87.09 86.92 87.59 90.72 90.69 90.3 89.55 88.94 88.41 87.82 87.07 86.82 86.4 86.02 85.66 85.32 85 84.67 83.94 82.83 81.95 81.19 80.48 78.86 69.47 68.77 70.06 73.95 75.8 77.79 81.57 83.07 84.34 85.1 85.25 84.26 83.63 86.44 85.3 84.1 83.36 82.48 81.58 80.47 79.34 82.13 81.69 80.7 79.88 79.16 78.38 77.42 76.47 75.46 74.48 78.27 80.7 79.91 78.75 77.78 81.14 81.08 80.03 78.91 78.01 76.9 75.97 81.93 80.27 78.67 77.42 76.16 74.7 76.39 76.04 74.65 73.29 71.79 74.39 74.91 74.54 73.08 72.75 71.32 70.38 70.35 70.01 69.36 67.77 69.26 69.8 68.38 67.62 68.39 66.95 65.21 66.64 63.45 60.66 62.34 60.32 58.64 60.46 58.59 61.87 61.85 67.44 77.06 91.74 93.15 94.15 93.11 91.51 89.96 88.16 86.98 88.03 86.24 84.65 83.23 81.7 80.25 78.8 77.51 76.2 75.04 74 75.49 77.14 76.15 76.27 78.19 76.49 77.31 76.65 74.99 73.51 72.07 70.59 71.96 76.29 74.86 74.93 71.9 71.01 77.47 75.78 76.6 76.07 74.57 73.02 72.65 73.16 71.53 69.78 67.98 69.96 72.16 70.47 68.86 67.37 65.87 72.16 71.34 69.93 68.44 67.16 66.01 67.25 70.91 69.75 68.59 67.48 66.31 64.81 66.58 65.97 64.7 64.7 60.94 59.08 58.42 57.77 57.11 53.31 49.96 49.4 48.84 48.3 47.74 47.24 46.76 46.29 48.9 49.23 48.53 48.03 54.34 53.79 53.24 52.96 52.17 51.7 58.55 78.2 77.03 76.19 77.15 75.87 95.47 109.67 112.28 112.01 107.93 105.96 105.06 102.98 102.2 105.23 101.85 99.89 96.23 94.76 91.51 91.63 91.54 85.23 87.83 87.38 84.44 85.19 84.03 86.73 102.52 104.45 106.98 107.02 99.26 94.45 113.44 157.33 147.38 171.89 171.95 132.71 126.02 121.18 115.45 110.48 117.85 117.63 124.65 109.59 111.27 99.78 98.21 99.2 97.97 89.55 87.91 93.34 94.42 93.2 90.29 91.46 89.98 88.35 88.41 82.44 79.89 75.69 75.66 84.5 96.73 87.48 82.39 83.48 79.31 78.16 72.77 72.45 68.46 67.62 68.76 70.07 68.55 65.3 58.96 59.17 62.37 66.28 55.62 55.23 55.85 56.75 50.89 53.88 52.95 55.08 53.61 58.78 61.85 55.91 53.32 46.41 44.57 50 50 53.36 46.23 50.45 49.07 45.85 48.45 49.96 46.53 50.51 47.58 48.05 46.84 47.67 49.16 55.54 55.82 58.22 56.19 57.77 63.19 54.76 55.74 62.54 61.39 69.6 79.23 80 93.68 107.63 100.18 97.3 90.45 80.64 80.58 75.82 85.59 89.35 89.42 104.73 95.32 89.27 90.44 86.97 79.98 81.22 87.35 83.64 82.22 94.4 102.18 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Dataseries Y: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
255 280.2 299.9 339.2 374.2 393.5 389.2 381.7 375.2 369 357.4 352.1 346.5 342.9 340.3 328.3 322.9 314.3 308.9 294 285.6 281.2 280.3 278.8 274.5 270.4 263.4 259.9 258 262.7 284.7 311.3 322.1 327 331.3 333.3 321.4 327 320 314.7 316.7 314.4 321.3 318.2 307.2 301.3 287.5 277.7 274.4 258.8 253.3 251 248.4 249.5 246.1 244.5 243.6 244 240.8 249.8 248 259.4 260.5 260.8 261.3 259.5 256.6 257.9 256.5 254.2 253.3 253.8 255.5 257.1 257.3 253.2 252.8 252 250.7 252.2 250 251 253.4 251.2 255.6 261.1 258.9 259.9 261.2 264.7 267.1 266.4 267.7 268.6 267.5 268.5 268.5 270.5 270.9 270.1 269.3 269.8 270.1 264.9 263.7 264.8 263.7 255.9 276.2 360.1 380.5 373.7 369.8 366.6 359.3 345.8 326.2 324.5 328.1 327.5 324.4 316.5 310.9 301.5 291.7 290.4 287.4 277.7 281.6 288 276 272.9 283 283.3 276.8 284.5 282.7 281.2 287.4 283.1 284 285.5 289.2 292.5 296.4 305.2 303.9 311.5 316.3 316.7 322.5 317.1 309.8 303.8 290.3 293.7 291.7 296.5 289.1 288.5 293.8 297.7 305.4 302.7 302.5 303 294.5 294.1 294.5 297.1 289.4 292.4 287.9 286.6 280.5 272.4 269.2 270.6 267.3 262.5 266.8 268.8 263.1 261.2 266 262.5 265.2 261.3 253.7 249.2 239.1 236.4 235.2 245.2 246.2 247.7 251.4 253.3 254.8 250 249.3 241.5 243.3 248 253 252.9 251.5 251.6 253.5 259.8 334.1 448 445.8 445 448.2 438.2 439.8 423.4 410.8 408.4 406.7 405.9 402.7 405.1 399.6 386.5 381.4 375.2 357.7 359 355 352.7 344.4 343.8 338 339 333.3 334.4 328.3 330.7 330 331.6 351.2 389.4 410.9 442.8 462.8 466.9 461.7 439.2 430.3 416.1 402.5 397.3 403.3 395.9 387.8 378.6 377.1 370.4 362 350.3 348.2 344.6 343.5 342.8 347.6 346.6 349.5 342.1 342 342.8 339.3 348.2 333.7 334.7 354 367.7 363.3 358.4 353.1 343.1 344.6 344.4 333.9 331.7 324.3 321.2 322.4 321.7 320.5 312.8 309.7 315.6 309.7 304.6 302.5 301.5 298.8 291.3 293.6 294.6 285.9 297.6 301.1 293.8 297.7 292.9 292.1 287.2 288.2 283.8 299.9 292.4 293.3 300.8 293.7 293.1 294.4 292.1 291.9 282.5 277.9 287.5 289.2 285.6 293.2 290.8 283.1 275 287.8 287.8 287.4 284 277.8 277.6 304.9 294 300.9 324 332.9 341.6 333.4 348.2 344.7 344.7 329.3 323.5 323.2 317.4 330.1 329.2 334.9 315.8 315.4 319.6 317.3 313.8 315.8 311.3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Tables (Output of Computation) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
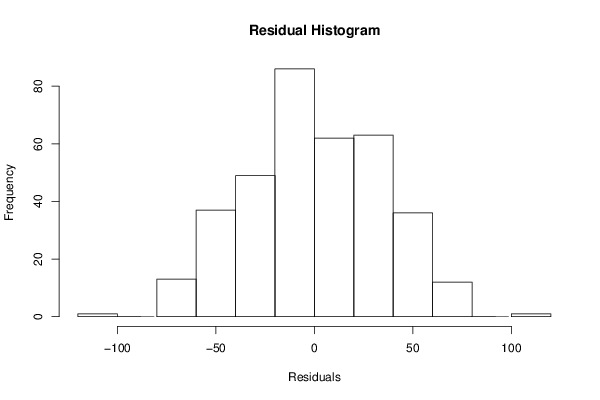
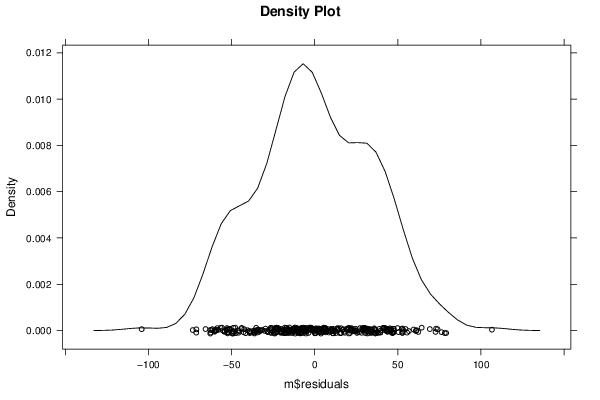
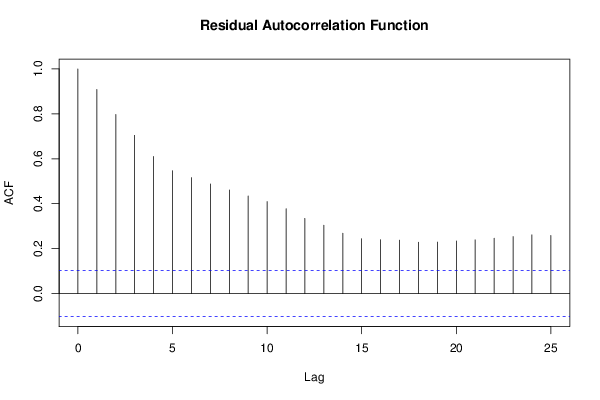
Figures (Output of Computation) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Input Parameters & R Code | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Parameters (Session): | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| par1 = 0 ; | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Parameters (R input): | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| par1 = 0 ; | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| R code (references can be found in the software module): | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
par1 <- as.numeric(par1) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||