Repository of Reproducible Computations

Free Statistics

of Irreproducible Research!

Author's title

Author

*The author of this computation has been verified*

R Software Module

rwasp_autocorrelation.wasp

Title produced by software

(Partial) Autocorrelation Function

Date of computation

Mon, 08 Dec 2008 13:00:12 -0700

Cite this page as follows

Statistical Computations at FreeStatistics.org, Office for Research Development and Education, URL https://freestatistics.org/blog/index.php?v=date/2008/Dec/08/t12287664591bhwjr70n49u9mj.htm/, Retrieved Thu, 31 Oct 2024 23:09:32 +0000

Statistical Computations at FreeStatistics.org, Office for Research Development and Education, URL https://freestatistics.org/blog/index.php?pk=30887, Retrieved Thu, 31 Oct 2024 23:09:32 +0000

QR Codes:

Paste this QR Code to cite your computation.

Original text written by user:

IsPrivate?

No (this computation is public)

User-defined keywords

Estimated Impact

182

Family? (F = Feedback message, R = changed R code, M = changed R Module, P = changed Parameters, D = changed Data)

F       [(Partial) Autocorrelation Function] [step 3] [2008-12-08 20:00:12] [6912578025c824de531bc660dd61b996] [Current]
F         [(Partial) Autocorrelation Function] [part 3] [2008-12-09 07:30:09] [b47fceb71c9525e79a89b5fc6d023d0e] 
-   P     [(Partial) Autocorrelation Function] [Hercomputatie fee...] [2008-12-12 21:39:27] [deb3c14ac9e4607a6d84fc9d0e0e6cc2] 

Feedback Forum

2008-12-12 21:40:46 [Kim Wester] [reply] 
Vergeet de lambda-waarde niet in te vullen!  
 
Herberekening met lambda-waarde 0,5: 
http://www.freestatistics.org/blog/index.php?v=date/2008/Dec/12/t12291180065ajrz9jcqf2spuz.htm
2008-12-13 11:57:47 [Kevin Engels] [reply] 
Wanneer we d en D gaan instellen op 1, mogen we weer niet vergeten de time lags op 60 in te stellen!  
 
http://www.freestatistics.org/blog/index.php?v=date/2008/Dec/07/t1228654489ncfa0492hqc02zw.htm
2008-12-13 13:01:54 [Ellen Smolders] [reply] 
De student heeft de juiste parameters ingevuld. Toevoeging:  
We zien dat er nog steeds een patroon aanwezig is. Dit patroon gaan we later wegwerken door een seizoenaal ARMA proces. We hebben de tijdreeks hier echter stationair gemaakt. Het lange termijn patroon en de meeste seizoenaliteit hebben we weggewerkt. 
2008-12-13 14:37:41 [An De Koninck] [reply] 
De lange termijntrend is in dit model volledig weggewerkt. Er is nog wel sprake van seizonaliteit. 
Deze zouden we kunnen wegwerken door paramter D te laten variëren. Deze staat echter al ingesteld op 1. Tijdens het hoorcollege en bij de VRM kwamen we echter al te weten dat het model waarbij d = 1 en D = 1 het beste is. Daarom wordt er niet verder gedifferentieerd. 
 
Om de resterende autocorrelatie weg te werken, kunnen de ARMA-modellen gebruikt worden. 
2008-12-15 13:20:03 [Kristof Augustyns] [reply] 
We kunnen hier stellen dat het om een AR proces gaat.  
Onze spectrum analyse uit voorgaande vragen bevestigt dit.  
 
De orde aflezen doen we via de partial autocorrelation.  
De eerste twee staafjes zijn significant verschillend van 0. Het derde is echter een twijfelgeval.  
We bekomen een p die gelijk is aan 3  
 
Om P te bepalen moeten we kijken naar seizoenaliteit. Lag 12 is significant, dus seizoenaliteit.  
P=0  
 
Voor de q kijken we naar de partial correlation. De eerste 5 staafjes zijn niet negatief en convergeren niet naar 0.  
q=0  
 
Voor de Q kijken we naar de partial correlation. We stellen duidelijke seizoenaliteit vast om de 12 lags.  
Voor de orde kijken we naar de autocorrelatie. Enkel lag 12 significant verschillend van 0, de rest niet.  
Q=1  
 
Samengevat bekomen we volgende waarden:  
Lambda = 0,5  
d = 1  
D = 1  
p = 3  
P = 0  
q = 0  
Q = 1 

Post a new message

Dataseries X:

Download CSV

Histogram

Boxplots

Summary of computational transaction
Raw Input	view raw input (R code)
Raw Output	view raw output of R engine
Computing time	3 seconds
R Server	'Herman Ole Andreas Wold' @ 193.190.124.10:1001

\begin{tabular}{lllllllll}
\hline
Summary of computational transaction \tabularnewline
Raw Input & view raw input (R code)  \tabularnewline
Raw Output & view raw output of R engine  \tabularnewline
Computing time & 3 seconds \tabularnewline
R Server & 'Herman Ole Andreas Wold' @ 193.190.124.10:1001 \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=30887&T=0

[TABLE]
[ROW][C]Summary of computational transaction[/C][/ROW]
[ROW][C]Raw Input[/C][C]view raw input (R code) [/C][/ROW]
[ROW][C]Raw Output[/C][C]view raw output of R engine [/C][/ROW]
[ROW][C]Computing time[/C][C]3 seconds[/C][/ROW]
[ROW][C]R Server[/C][C]'Herman Ole Andreas Wold' @ 193.190.124.10:1001[/C][/ROW]
[/TABLE]
Source: https://freestatistics.org/blog/index.php?pk=30887&T=0

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=30887&T=0

As an alternative you can also use a QR Code:

The GUIDs for individual cells are displayed in the table below:

Summary of computational transaction
Raw Input	view raw input (R code)
Raw Output	view raw output of R engine
Computing time	3 seconds
R Server	'Herman Ole Andreas Wold' @ 193.190.124.10:1001

Autocorrelation Function
Time lag k	ACF(k)	T-STAT	P-value
1	0.210141	3.9816	4.1e-05
2	0.325131	6.1603	0
3	0.153275	2.9041	0.001955
4	0.167252	3.169	0.000831
5	0.099156	1.8787	0.030545
6	0.064513	1.2223	0.111191
7	-0.057203	-1.0838	0.13958
8	-0.023244	-0.4404	0.329956
9	-0.085115	-1.6127	0.053845
10	-0.168424	-3.1912	0.000771
11	-0.075939	-1.4388	0.075533
12	-0.475334	-9.0063	0
13	-0.179215	-3.3956	0.000381
14	-0.162819	-3.085	0.001097
15	-0.106644	-2.0206	0.02203
16	-0.147945	-2.8032	0.002668
17	-0.091478	-1.7333	0.041954
18	-0.089745	-1.7004	0.044958
19	0.027328	0.5178	0.302458
20	-0.012913	-0.2447	0.403425
21	0.024199	0.4585	0.323437
22	-0.018741	-0.3551	0.361367
23	0.009567	0.1813	0.42813
24	-0.022226	-0.4211	0.336957
25	0.091974	1.7427	0.041125

\begin{tabular}{lllllllll}
\hline
Autocorrelation Function \tabularnewline
Time lag k & ACF(k) & T-STAT & P-value \tabularnewline
1 & 0.210141 & 3.9816 & 4.1e-05 \tabularnewline
2 & 0.325131 & 6.1603 & 0 \tabularnewline
3 & 0.153275 & 2.9041 & 0.001955 \tabularnewline
4 & 0.167252 & 3.169 & 0.000831 \tabularnewline
5 & 0.099156 & 1.8787 & 0.030545 \tabularnewline
6 & 0.064513 & 1.2223 & 0.111191 \tabularnewline
7 & -0.057203 & -1.0838 & 0.13958 \tabularnewline
8 & -0.023244 & -0.4404 & 0.329956 \tabularnewline
9 & -0.085115 & -1.6127 & 0.053845 \tabularnewline
10 & -0.168424 & -3.1912 & 0.000771 \tabularnewline
11 & -0.075939 & -1.4388 & 0.075533 \tabularnewline
12 & -0.475334 & -9.0063 & 0 \tabularnewline
13 & -0.179215 & -3.3956 & 0.000381 \tabularnewline
14 & -0.162819 & -3.085 & 0.001097 \tabularnewline
15 & -0.106644 & -2.0206 & 0.02203 \tabularnewline
16 & -0.147945 & -2.8032 & 0.002668 \tabularnewline
17 & -0.091478 & -1.7333 & 0.041954 \tabularnewline
18 & -0.089745 & -1.7004 & 0.044958 \tabularnewline
19 & 0.027328 & 0.5178 & 0.302458 \tabularnewline
20 & -0.012913 & -0.2447 & 0.403425 \tabularnewline
21 & 0.024199 & 0.4585 & 0.323437 \tabularnewline
22 & -0.018741 & -0.3551 & 0.361367 \tabularnewline
23 & 0.009567 & 0.1813 & 0.42813 \tabularnewline
24 & -0.022226 & -0.4211 & 0.336957 \tabularnewline
25 & 0.091974 & 1.7427 & 0.041125 \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=30887&T=1

[TABLE]
[ROW][C]Autocorrelation Function[/C][/ROW]
[ROW][C]Time lag k[/C][C]ACF(k)[/C][C]T-STAT[/C][C]P-value[/C][/ROW]
[ROW][C]1[/C][C]0.210141[/C][C]3.9816[/C][C]4.1e-05[/C][/ROW]
[ROW][C]2[/C][C]0.325131[/C][C]6.1603[/C][C]0[/C][/ROW]
[ROW][C]3[/C][C]0.153275[/C][C]2.9041[/C][C]0.001955[/C][/ROW]
[ROW][C]4[/C][C]0.167252[/C][C]3.169[/C][C]0.000831[/C][/ROW]
[ROW][C]5[/C][C]0.099156[/C][C]1.8787[/C][C]0.030545[/C][/ROW]
[ROW][C]6[/C][C]0.064513[/C][C]1.2223[/C][C]0.111191[/C][/ROW]
[ROW][C]7[/C][C]-0.057203[/C][C]-1.0838[/C][C]0.13958[/C][/ROW]
[ROW][C]8[/C][C]-0.023244[/C][C]-0.4404[/C][C]0.329956[/C][/ROW]
[ROW][C]9[/C][C]-0.085115[/C][C]-1.6127[/C][C]0.053845[/C][/ROW]
[ROW][C]10[/C][C]-0.168424[/C][C]-3.1912[/C][C]0.000771[/C][/ROW]
[ROW][C]11[/C][C]-0.075939[/C][C]-1.4388[/C][C]0.075533[/C][/ROW]
[ROW][C]12[/C][C]-0.475334[/C][C]-9.0063[/C][C]0[/C][/ROW]
[ROW][C]13[/C][C]-0.179215[/C][C]-3.3956[/C][C]0.000381[/C][/ROW]
[ROW][C]14[/C][C]-0.162819[/C][C]-3.085[/C][C]0.001097[/C][/ROW]
[ROW][C]15[/C][C]-0.106644[/C][C]-2.0206[/C][C]0.02203[/C][/ROW]
[ROW][C]16[/C][C]-0.147945[/C][C]-2.8032[/C][C]0.002668[/C][/ROW]
[ROW][C]17[/C][C]-0.091478[/C][C]-1.7333[/C][C]0.041954[/C][/ROW]
[ROW][C]18[/C][C]-0.089745[/C][C]-1.7004[/C][C]0.044958[/C][/ROW]
[ROW][C]19[/C][C]0.027328[/C][C]0.5178[/C][C]0.302458[/C][/ROW]
[ROW][C]20[/C][C]-0.012913[/C][C]-0.2447[/C][C]0.403425[/C][/ROW]
[ROW][C]21[/C][C]0.024199[/C][C]0.4585[/C][C]0.323437[/C][/ROW]
[ROW][C]22[/C][C]-0.018741[/C][C]-0.3551[/C][C]0.361367[/C][/ROW]
[ROW][C]23[/C][C]0.009567[/C][C]0.1813[/C][C]0.42813[/C][/ROW]
[ROW][C]24[/C][C]-0.022226[/C][C]-0.4211[/C][C]0.336957[/C][/ROW]
[ROW][C]25[/C][C]0.091974[/C][C]1.7427[/C][C]0.041125[/C][/ROW]
[/TABLE]
Source: https://freestatistics.org/blog/index.php?pk=30887&T=1

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=30887&T=1

As an alternative you can also use a QR Code:

The GUIDs for individual cells are displayed in the table below:

Autocorrelation Function
Time lag k	ACF(k)	T-STAT	P-value
1	0.210141	3.9816	4.1e-05
2	0.325131	6.1603	0
3	0.153275	2.9041	0.001955
4	0.167252	3.169	0.000831
5	0.099156	1.8787	0.030545
6	0.064513	1.2223	0.111191
7	-0.057203	-1.0838	0.13958
8	-0.023244	-0.4404	0.329956
9	-0.085115	-1.6127	0.053845
10	-0.168424	-3.1912	0.000771
11	-0.075939	-1.4388	0.075533
12	-0.475334	-9.0063	0
13	-0.179215	-3.3956	0.000381
14	-0.162819	-3.085	0.001097
15	-0.106644	-2.0206	0.02203
16	-0.147945	-2.8032	0.002668
17	-0.091478	-1.7333	0.041954
18	-0.089745	-1.7004	0.044958
19	0.027328	0.5178	0.302458
20	-0.012913	-0.2447	0.403425
21	0.024199	0.4585	0.323437
22	-0.018741	-0.3551	0.361367
23	0.009567	0.1813	0.42813
24	-0.022226	-0.4211	0.336957
25	0.091974	1.7427	0.041125

Partial Autocorrelation Function
Time lag k	PACF(k)	T-STAT	P-value
1	0.210141	3.9816	4.1e-05
2	0.293952	5.5696	0
3	0.049544	0.9387	0.174253
4	0.049534	0.9385	0.174302
5	0.012741	0.2414	0.404686
6	-0.02095	-0.3969	0.34582
7	-0.124687	-2.3625	0.009343
8	-0.032709	-0.6197	0.267912
9	-0.045438	-0.8609	0.194928
10	-0.146092	-2.768	0.002966
11	0.023631	0.4477	0.327306
12	-0.42914	-8.131	0
13	-0.0237	-0.449	0.326836
14	0.150889	2.8589	0.002249
15	0.029791	0.5645	0.286395
16	-0.044612	-0.8453	0.199257
17	-0.012037	-0.2281	0.40986
18	0.004648	0.0881	0.464938
19	0.011303	0.2142	0.415271
20	0.009823	0.1861	0.426229
21	-0.009818	-0.186	0.426268
22	-0.15669	-2.9689	0.001595
23	0.012173	0.2306	0.408859
24	-0.273087	-5.1743	0
25	0.053216	1.0083	0.156993

\begin{tabular}{lllllllll}
\hline
Partial Autocorrelation Function \tabularnewline
Time lag k & PACF(k) & T-STAT & P-value \tabularnewline
1 & 0.210141 & 3.9816 & 4.1e-05 \tabularnewline
2 & 0.293952 & 5.5696 & 0 \tabularnewline
3 & 0.049544 & 0.9387 & 0.174253 \tabularnewline
4 & 0.049534 & 0.9385 & 0.174302 \tabularnewline
5 & 0.012741 & 0.2414 & 0.404686 \tabularnewline
6 & -0.02095 & -0.3969 & 0.34582 \tabularnewline
7 & -0.124687 & -2.3625 & 0.009343 \tabularnewline
8 & -0.032709 & -0.6197 & 0.267912 \tabularnewline
9 & -0.045438 & -0.8609 & 0.194928 \tabularnewline
10 & -0.146092 & -2.768 & 0.002966 \tabularnewline
11 & 0.023631 & 0.4477 & 0.327306 \tabularnewline
12 & -0.42914 & -8.131 & 0 \tabularnewline
13 & -0.0237 & -0.449 & 0.326836 \tabularnewline
14 & 0.150889 & 2.8589 & 0.002249 \tabularnewline
15 & 0.029791 & 0.5645 & 0.286395 \tabularnewline
16 & -0.044612 & -0.8453 & 0.199257 \tabularnewline
17 & -0.012037 & -0.2281 & 0.40986 \tabularnewline
18 & 0.004648 & 0.0881 & 0.464938 \tabularnewline
19 & 0.011303 & 0.2142 & 0.415271 \tabularnewline
20 & 0.009823 & 0.1861 & 0.426229 \tabularnewline
21 & -0.009818 & -0.186 & 0.426268 \tabularnewline
22 & -0.15669 & -2.9689 & 0.001595 \tabularnewline
23 & 0.012173 & 0.2306 & 0.408859 \tabularnewline
24 & -0.273087 & -5.1743 & 0 \tabularnewline
25 & 0.053216 & 1.0083 & 0.156993 \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=30887&T=2

[TABLE]
[ROW][C]Partial Autocorrelation Function[/C][/ROW]
[ROW][C]Time lag k[/C][C]PACF(k)[/C][C]T-STAT[/C][C]P-value[/C][/ROW]
[ROW][C]1[/C][C]0.210141[/C][C]3.9816[/C][C]4.1e-05[/C][/ROW]
[ROW][C]2[/C][C]0.293952[/C][C]5.5696[/C][C]0[/C][/ROW]
[ROW][C]3[/C][C]0.049544[/C][C]0.9387[/C][C]0.174253[/C][/ROW]
[ROW][C]4[/C][C]0.049534[/C][C]0.9385[/C][C]0.174302[/C][/ROW]
[ROW][C]5[/C][C]0.012741[/C][C]0.2414[/C][C]0.404686[/C][/ROW]
[ROW][C]6[/C][C]-0.02095[/C][C]-0.3969[/C][C]0.34582[/C][/ROW]
[ROW][C]7[/C][C]-0.124687[/C][C]-2.3625[/C][C]0.009343[/C][/ROW]
[ROW][C]8[/C][C]-0.032709[/C][C]-0.6197[/C][C]0.267912[/C][/ROW]
[ROW][C]9[/C][C]-0.045438[/C][C]-0.8609[/C][C]0.194928[/C][/ROW]
[ROW][C]10[/C][C]-0.146092[/C][C]-2.768[/C][C]0.002966[/C][/ROW]
[ROW][C]11[/C][C]0.023631[/C][C]0.4477[/C][C]0.327306[/C][/ROW]
[ROW][C]12[/C][C]-0.42914[/C][C]-8.131[/C][C]0[/C][/ROW]
[ROW][C]13[/C][C]-0.0237[/C][C]-0.449[/C][C]0.326836[/C][/ROW]
[ROW][C]14[/C][C]0.150889[/C][C]2.8589[/C][C]0.002249[/C][/ROW]
[ROW][C]15[/C][C]0.029791[/C][C]0.5645[/C][C]0.286395[/C][/ROW]
[ROW][C]16[/C][C]-0.044612[/C][C]-0.8453[/C][C]0.199257[/C][/ROW]
[ROW][C]17[/C][C]-0.012037[/C][C]-0.2281[/C][C]0.40986[/C][/ROW]
[ROW][C]18[/C][C]0.004648[/C][C]0.0881[/C][C]0.464938[/C][/ROW]
[ROW][C]19[/C][C]0.011303[/C][C]0.2142[/C][C]0.415271[/C][/ROW]
[ROW][C]20[/C][C]0.009823[/C][C]0.1861[/C][C]0.426229[/C][/ROW]
[ROW][C]21[/C][C]-0.009818[/C][C]-0.186[/C][C]0.426268[/C][/ROW]
[ROW][C]22[/C][C]-0.15669[/C][C]-2.9689[/C][C]0.001595[/C][/ROW]
[ROW][C]23[/C][C]0.012173[/C][C]0.2306[/C][C]0.408859[/C][/ROW]
[ROW][C]24[/C][C]-0.273087[/C][C]-5.1743[/C][C]0[/C][/ROW]
[ROW][C]25[/C][C]0.053216[/C][C]1.0083[/C][C]0.156993[/C][/ROW]
[/TABLE]
Source: https://freestatistics.org/blog/index.php?pk=30887&T=2

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=30887&T=2

As an alternative you can also use a QR Code:

The GUIDs for individual cells are displayed in the table below:

Partial Autocorrelation Function
Time lag k	PACF(k)	T-STAT	P-value
1	0.210141	3.9816	4.1e-05
2	0.293952	5.5696	0
3	0.049544	0.9387	0.174253
4	0.049534	0.9385	0.174302
5	0.012741	0.2414	0.404686
6	-0.02095	-0.3969	0.34582
7	-0.124687	-2.3625	0.009343
8	-0.032709	-0.6197	0.267912
9	-0.045438	-0.8609	0.194928
10	-0.146092	-2.768	0.002966
11	0.023631	0.4477	0.327306
12	-0.42914	-8.131	0
13	-0.0237	-0.449	0.326836
14	0.150889	2.8589	0.002249
15	0.029791	0.5645	0.286395
16	-0.044612	-0.8453	0.199257
17	-0.012037	-0.2281	0.40986
18	0.004648	0.0881	0.464938
19	0.011303	0.2142	0.415271
20	0.009823	0.1861	0.426229
21	-0.009818	-0.186	0.426268
22	-0.15669	-2.9689	0.001595
23	0.012173	0.2306	0.408859
24	-0.273087	-5.1743	0
25	0.053216	1.0083	0.156993

Figure 1

PNG link

Postscript link

PDF link

Figure 2

PNG link

Postscript link

PDF link

Parameters (Session):

par1 = Default ; par2 = 1 ; par3 = 1 ; par4 = 1 ; par5 = 12 ;

Parameters (R input):

par1 = Default ; par2 = 1 ; par3 = 1 ; par4 = 1 ; par5 = 12 ;

R code (references can be found in the software module):

if (par1 == 'Default') {
par1 = 10*log10(length(x))
} else {
par1 <- as.numeric(par1)
}
par2 <- as.numeric(par2)
par3 <- as.numeric(par3)
par4 <- as.numeric(par4)
par5 <- as.numeric(par5)
if (par2 == 0) {
x <- log(x)
} else {
x <- (x ^ par2 - 1) / par2
}
if (par3 > 0) x <- diff(x,lag=1,difference=par3)
if (par4 > 0) x <- diff(x,lag=par5,difference=par4)
bitmap(file='pic1.png')
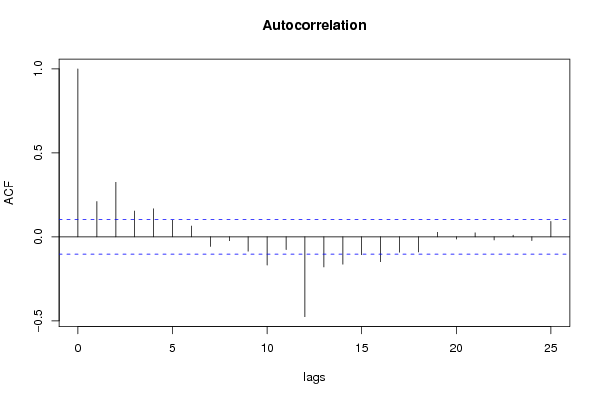
racf <- acf(x,par1,main='Autocorrelation',xlab='lags',ylab='ACF')
dev.off()
bitmap(file='pic2.png')
rpacf <- pacf(x,par1,main='Partial Autocorrelation',xlab='lags',ylab='PACF')
dev.off()
(myacf <- c(racf$acf))
(mypacf <- c(rpacf$acf))
lengthx <- length(x)
sqrtn <- sqrt(lengthx)
load(file='createtable')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a,'Autocorrelation Function',4,TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'Time lag k',header=TRUE)
a<-table.element(a,hyperlink('basics.htm','ACF(k)','click here for more information about the Autocorrelation Function'),header=TRUE)
a<-table.element(a,'T-STAT',header=TRUE)
a<-table.element(a,'P-value',header=TRUE)
a<-table.row.end(a)
for (i in 2:(par1+1)) {
a<-table.row.start(a)
a<-table.element(a,i-1,header=TRUE)
a<-table.element(a,round(myacf[i],6))
mytstat <- myacf[i]*sqrtn
a<-table.element(a,round(mytstat,4))
a<-table.element(a,round(1-pt(abs(mytstat),lengthx),6))
a<-table.row.end(a)
}
a<-table.end(a)
table.save(a,file='mytable.tab')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a,'Partial Autocorrelation Function',4,TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'Time lag k',header=TRUE)
a<-table.element(a,hyperlink('basics.htm','PACF(k)','click here for more information about the Partial Autocorrelation Function'),header=TRUE)
a<-table.element(a,'T-STAT',header=TRUE)
a<-table.element(a,'P-value',header=TRUE)
a<-table.row.end(a)
for (i in 1:par1) {
a<-table.row.start(a)
a<-table.element(a,i,header=TRUE)
a<-table.element(a,round(mypacf[i],6))
mytstat <- mypacf[i]*sqrtn
a<-table.element(a,round(mytstat,4))
a<-table.element(a,round(1-pt(abs(mytstat),lengthx),6))
a<-table.row.end(a)
}
a<-table.end(a)
table.save(a,file='mytable1.tab')

Free Statistics

Description of Statistical Computation

Tree of Dependent Computations

Dataset

Tables (Output of Computation)

Figures (Output of Computation)

Input Parameters & R Code