Repository of Reproducible Computations

Free Statistics

of Irreproducible Research!

Author's title

Author

*The author of this computation has been verified*

R Software Module

rwasp_Two Factor ANOVA.wasp

Title produced by software

Two-Way ANOVA

Date of computation

Thu, 27 Oct 2011 07:16:49 -0400

Cite this page as follows

Statistical Computations at FreeStatistics.org, Office for Research Development and Education, URL https://freestatistics.org/blog/index.php?v=date/2011/Oct/27/t1319714226hhxm0830uyvl8ug.htm/, Retrieved Fri, 01 Nov 2024 00:09:14 +0000

Statistical Computations at FreeStatistics.org, Office for Research Development and Education, URL https://freestatistics.org/blog/index.php?pk=136829, Retrieved Fri, 01 Nov 2024 00:09:14 +0000

QR Codes:

Paste this QR Code to cite your computation.

Original text written by user:

IsPrivate?

No (this computation is public)

User-defined keywords

Estimated Impact

210

Family? (F = Feedback message, R = changed R code, M = changed R Module, P = changed Parameters, D = changed Data)

-     [Two-Way ANOVA] [Golfballs] [2010-10-25 12:43:22] [b98453cac15ba1066b407e146608df68]
F R PD  [Two-Way ANOVA] [WS5 Q8] [2010-11-01 20:06:21] [b11c112f8986de933f8b95cd30e75cc2]
-         [Two-Way ANOVA] [] [2010-11-02 13:06:43] [d87a19cd5db53e12ea62bda70b3bb267]
F   P       [Two-Way ANOVA] [] [2010-11-16 20:11:08] [42a441ca3193af442aa2201743dfb347]
-   PD          [Two-Way ANOVA] [Question 8] [2011-10-27 11:16:49] [d519577d845e738b812f706f10c86f64] [Current]

Feedback Forum

Post a new message

Dataseries X:

Download CSV

Histogram

Boxplots

'F'	0	1
'F'	0	0
'H'	0	0
'E'	0	1
'E'	1	1
'H'	0	1
'E'	1	1
'F'	1	1
'E'	0	1
'F'	1	0
'H'	0	0
'E'	1	0
'F'	1	0
'F'	1	0
'F'	0	0
'F'	1	0
'H'	1	1
'E'	1	0
'E'	0	0
'H'	0	0
'E'	1	1
'F'	0	1
'F'	0	0
'H'	0	0
'E'	0	1
'F'	1	1
'E'	1	1
'H'	0	1
'H'	0	1
'H'	0	1
'E'	0	1
'H'	0	0
'E'	1	0
'H'	0	1
'F'	0	1
'H'	0	1
'F'	1	0
'E'	0	1
'E'	1	1
'F'	0	0
'H'	0	1
'F'	0	0
'E'	0	1
'E'	-1	1
'H'	0	0
'H'	0	1
'F'	0	1
'H'	0	1
'E'	1	0
'F'	0	1
'E'	1	0
'E'	0	0
'E'	0	0
'F'	0	1
'E'	0	1
'F'	1	1
'H'	0	1
'H'	0	1
'H'	0	1
'F'	0	0
'H'	0	1
'H'	0	1
'F'	1	1
'F'	1	1
'H'	0	0
'F'	0	1
'H'	0	1
'E'	0	0
'F'	1	1
'E'	0	0
'H'	0	1
'F'	1	1
'F'	0	1
'H'	0	1
'E'	1	1
'F'	0	0
'H'	0	1
'E'	0	1
'F'	0	0
'H'	0	0
'H'	0	1
'F'	1	1
'F'	1	1
'H'	0	1
'E'	0	0
'H'	0	1
'E'	0	1
'E'	0	0
'F'	0	1
'F'	0	1

Summary of computational transaction
Raw Input	view raw input (R code)
Raw Output	view raw output of R engine
Computing time	2 seconds
R Server	'Gwilym Jenkins' @ jenkins.wessa.net

\begin{tabular}{lllllllll}
\hline
Summary of computational transaction \tabularnewline
Raw Input & view raw input (R code)  \tabularnewline
Raw Output & view raw output of R engine  \tabularnewline
Computing time & 2 seconds \tabularnewline
R Server & 'Gwilym Jenkins' @ jenkins.wessa.net \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=136829&T=0

[TABLE]
[ROW][C]Summary of computational transaction[/C][/ROW]
[ROW][C]Raw Input[/C][C]view raw input (R code) [/C][/ROW]
[ROW][C]Raw Output[/C][C]view raw output of R engine [/C][/ROW]
[ROW][C]Computing time[/C][C]2 seconds[/C][/ROW]
[ROW][C]R Server[/C][C]'Gwilym Jenkins' @ jenkins.wessa.net[/C][/ROW]
[/TABLE]
Source: https://freestatistics.org/blog/index.php?pk=136829&T=0

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=136829&T=0

As an alternative you can also use a QR Code:

The GUIDs for individual cells are displayed in the table below:

Summary of computational transaction
Raw Input	view raw input (R code)
Raw Output	view raw output of R engine
Computing time	2 seconds
R Server	'Gwilym Jenkins' @ jenkins.wessa.net

ANOVA Model
Response ~ Treatment_A * Treatment_B
means	0.417	-0.032	-0.417	-0.104	0.193	0.15

\begin{tabular}{lllllllll}
\hline
ANOVA Model \tabularnewline
Response ~ Treatment_A * Treatment_B \tabularnewline
means & 0.417 & -0.032 & -0.417 & -0.104 & 0.193 & 0.15 \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=136829&T=1

[TABLE]
[ROW][C]ANOVA Model[/C][/ROW]
[ROW][C]Response ~ Treatment_A * Treatment_B[/C][/ROW]
[ROW][C]means[/C][C]0.417[/C][C]-0.032[/C][C]-0.417[/C][C]-0.104[/C][C]0.193[/C][C]0.15[/C][/ROW]
[/TABLE]
Source: https://freestatistics.org/blog/index.php?pk=136829&T=1

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=136829&T=1

As an alternative you can also use a QR Code:

The GUIDs for individual cells are displayed in the table below:

ANOVA Model
Response ~ Treatment_A * Treatment_B
means	0.417	-0.032	-0.417	-0.104	0.193	0.15

ANOVA Statistics
	Df	Sum Sq	Mean Sq	F value	Pr(>F)
	2
Treatment_A	2	2.785	1.393	6.832	0.002
Treatment_B	2	0.003	0.003	0.014	0.907
Treatment_A:Treatment_B	2	0.145	0.072	0.356	0.702
Residuals	84	17.122	0.204

\begin{tabular}{lllllllll}
\hline
ANOVA Statistics \tabularnewline
  & Df & Sum Sq & Mean Sq & F value & Pr(>F) \tabularnewline
 & 2 &  &  &  &  \tabularnewline
Treatment_A & 2 & 2.785 & 1.393 & 6.832 & 0.002 \tabularnewline
Treatment_B & 2 & 0.003 & 0.003 & 0.014 & 0.907 \tabularnewline
Treatment_A:Treatment_B & 2 & 0.145 & 0.072 & 0.356 & 0.702 \tabularnewline
Residuals & 84 & 17.122 & 0.204 &   &   \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=136829&T=2

[TABLE]
[ROW][C]ANOVA Statistics[/C][/ROW]
[ROW][C] [/C][C]Df[/C][C]Sum Sq[/C][C]Mean Sq[/C][C]F value[/C][C]Pr(>F)[/C][/ROW]
[ROW][C][/C][C]2[/C][C][/C][C][/C][C][/C][C][/C][/ROW]
[ROW][C]Treatment_A[/C][C]2[/C][C]2.785[/C][C]1.393[/C][C]6.832[/C][C]0.002[/C][/ROW]
[ROW][C]Treatment_B[/C][C]2[/C][C]0.003[/C][C]0.003[/C][C]0.014[/C][C]0.907[/C][/ROW]
[ROW][C]Treatment_A:Treatment_B[/C][C]2[/C][C]0.145[/C][C]0.072[/C][C]0.356[/C][C]0.702[/C][/ROW]
[ROW][C]Residuals[/C][C]84[/C][C]17.122[/C][C]0.204[/C][C] [/C][C] [/C][/ROW]
[/TABLE]
Source: https://freestatistics.org/blog/index.php?pk=136829&T=2

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=136829&T=2

As an alternative you can also use a QR Code:

The GUIDs for individual cells are displayed in the table below:

ANOVA Statistics
	Df	Sum Sq	Mean Sq	F value	Pr(>F)
	2
Treatment_A	2	2.785	1.393	6.832	0.002
Treatment_B	2	0.003	0.003	0.014	0.907
Treatment_A:Treatment_B	2	0.145	0.072	0.356	0.702
Residuals	84	17.122	0.204

Tukey Honest Significant Difference Comparisons
	diff	lwr	upr	p adj
F-E	0.08	-0.198	0.359	0.771
H-E	-0.324	-0.607	-0.041	0.021
H-F	-0.404	-0.678	-0.13	0.002
1-0	0.011	-0.185	0.208	0.908
F:0-E:0	-0.032	-0.559	0.495	1
H:0-E:0	-0.417	-1.018	0.184	0.339
E:1-E:0	-0.104	-0.607	0.399	0.99
F:1-E:0	0.057	-0.429	0.543	0.999
H:1-E:0	-0.371	-0.844	0.101	0.209
H:0-F:0	-0.385	-0.976	0.207	0.412
E:1-F:0	-0.072	-0.564	0.42	0.998
F:1-F:0	0.089	-0.385	0.563	0.994
H:1-F:0	-0.339	-0.8	0.121	0.274
E:1-H:0	0.312	-0.258	0.883	0.602
F:1-H:0	0.474	-0.081	1.029	0.139
H:1-H:0	0.045	-0.498	0.589	1
F:1-E:1	0.161	-0.286	0.608	0.899
H:1-E:1	-0.267	-0.7	0.166	0.471
H:1-F:1	-0.428	-0.841	-0.016	0.037

\begin{tabular}{lllllllll}
\hline
Tukey Honest Significant Difference Comparisons \tabularnewline
  & diff & lwr & upr & p adj \tabularnewline
F-E & 0.08 & -0.198 & 0.359 & 0.771 \tabularnewline
H-E & -0.324 & -0.607 & -0.041 & 0.021 \tabularnewline
H-F & -0.404 & -0.678 & -0.13 & 0.002 \tabularnewline
1-0 & 0.011 & -0.185 & 0.208 & 0.908 \tabularnewline
F:0-E:0 & -0.032 & -0.559 & 0.495 & 1 \tabularnewline
H:0-E:0 & -0.417 & -1.018 & 0.184 & 0.339 \tabularnewline
E:1-E:0 & -0.104 & -0.607 & 0.399 & 0.99 \tabularnewline
F:1-E:0 & 0.057 & -0.429 & 0.543 & 0.999 \tabularnewline
H:1-E:0 & -0.371 & -0.844 & 0.101 & 0.209 \tabularnewline
H:0-F:0 & -0.385 & -0.976 & 0.207 & 0.412 \tabularnewline
E:1-F:0 & -0.072 & -0.564 & 0.42 & 0.998 \tabularnewline
F:1-F:0 & 0.089 & -0.385 & 0.563 & 0.994 \tabularnewline
H:1-F:0 & -0.339 & -0.8 & 0.121 & 0.274 \tabularnewline
E:1-H:0 & 0.312 & -0.258 & 0.883 & 0.602 \tabularnewline
F:1-H:0 & 0.474 & -0.081 & 1.029 & 0.139 \tabularnewline
H:1-H:0 & 0.045 & -0.498 & 0.589 & 1 \tabularnewline
F:1-E:1 & 0.161 & -0.286 & 0.608 & 0.899 \tabularnewline
H:1-E:1 & -0.267 & -0.7 & 0.166 & 0.471 \tabularnewline
H:1-F:1 & -0.428 & -0.841 & -0.016 & 0.037 \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=136829&T=3

[TABLE]
[ROW][C]Tukey Honest Significant Difference Comparisons[/C][/ROW]
[ROW][C] [/C][C]diff[/C][C]lwr[/C][C]upr[/C][C]p adj[/C][/ROW]
[ROW][C]F-E[/C][C]0.08[/C][C]-0.198[/C][C]0.359[/C][C]0.771[/C][/ROW]
[ROW][C]H-E[/C][C]-0.324[/C][C]-0.607[/C][C]-0.041[/C][C]0.021[/C][/ROW]
[ROW][C]H-F[/C][C]-0.404[/C][C]-0.678[/C][C]-0.13[/C][C]0.002[/C][/ROW]
[ROW][C]1-0[/C][C]0.011[/C][C]-0.185[/C][C]0.208[/C][C]0.908[/C][/ROW]
[ROW][C]F:0-E:0[/C][C]-0.032[/C][C]-0.559[/C][C]0.495[/C][C]1[/C][/ROW]
[ROW][C]H:0-E:0[/C][C]-0.417[/C][C]-1.018[/C][C]0.184[/C][C]0.339[/C][/ROW]
[ROW][C]E:1-E:0[/C][C]-0.104[/C][C]-0.607[/C][C]0.399[/C][C]0.99[/C][/ROW]
[ROW][C]F:1-E:0[/C][C]0.057[/C][C]-0.429[/C][C]0.543[/C][C]0.999[/C][/ROW]
[ROW][C]H:1-E:0[/C][C]-0.371[/C][C]-0.844[/C][C]0.101[/C][C]0.209[/C][/ROW]
[ROW][C]H:0-F:0[/C][C]-0.385[/C][C]-0.976[/C][C]0.207[/C][C]0.412[/C][/ROW]
[ROW][C]E:1-F:0[/C][C]-0.072[/C][C]-0.564[/C][C]0.42[/C][C]0.998[/C][/ROW]
[ROW][C]F:1-F:0[/C][C]0.089[/C][C]-0.385[/C][C]0.563[/C][C]0.994[/C][/ROW]
[ROW][C]H:1-F:0[/C][C]-0.339[/C][C]-0.8[/C][C]0.121[/C][C]0.274[/C][/ROW]
[ROW][C]E:1-H:0[/C][C]0.312[/C][C]-0.258[/C][C]0.883[/C][C]0.602[/C][/ROW]
[ROW][C]F:1-H:0[/C][C]0.474[/C][C]-0.081[/C][C]1.029[/C][C]0.139[/C][/ROW]
[ROW][C]H:1-H:0[/C][C]0.045[/C][C]-0.498[/C][C]0.589[/C][C]1[/C][/ROW]
[ROW][C]F:1-E:1[/C][C]0.161[/C][C]-0.286[/C][C]0.608[/C][C]0.899[/C][/ROW]
[ROW][C]H:1-E:1[/C][C]-0.267[/C][C]-0.7[/C][C]0.166[/C][C]0.471[/C][/ROW]
[ROW][C]H:1-F:1[/C][C]-0.428[/C][C]-0.841[/C][C]-0.016[/C][C]0.037[/C][/ROW]
[/TABLE]
Source: https://freestatistics.org/blog/index.php?pk=136829&T=3

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=136829&T=3

As an alternative you can also use a QR Code:

The GUIDs for individual cells are displayed in the table below:

Tukey Honest Significant Difference Comparisons
	diff	lwr	upr	p adj
F-E	0.08	-0.198	0.359	0.771
H-E	-0.324	-0.607	-0.041	0.021
H-F	-0.404	-0.678	-0.13	0.002
1-0	0.011	-0.185	0.208	0.908
F:0-E:0	-0.032	-0.559	0.495	1
H:0-E:0	-0.417	-1.018	0.184	0.339
E:1-E:0	-0.104	-0.607	0.399	0.99
F:1-E:0	0.057	-0.429	0.543	0.999
H:1-E:0	-0.371	-0.844	0.101	0.209
H:0-F:0	-0.385	-0.976	0.207	0.412
E:1-F:0	-0.072	-0.564	0.42	0.998
F:1-F:0	0.089	-0.385	0.563	0.994
H:1-F:0	-0.339	-0.8	0.121	0.274
E:1-H:0	0.312	-0.258	0.883	0.602
F:1-H:0	0.474	-0.081	1.029	0.139
H:1-H:0	0.045	-0.498	0.589	1
F:1-E:1	0.161	-0.286	0.608	0.899
H:1-E:1	-0.267	-0.7	0.166	0.471
H:1-F:1	-0.428	-0.841	-0.016	0.037

Levenes Test for Homogeneity of Variance
	Df	F value	Pr(>F)
Group	5	3.525	0.006
	84

\begin{tabular}{lllllllll}
\hline
Levenes Test for Homogeneity of Variance \tabularnewline
  & Df & F value & Pr(>F) \tabularnewline
Group & 5 & 3.525 & 0.006 \tabularnewline
  & 84 &   &   \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=136829&T=4

[TABLE]
[ROW][C]Levenes Test for Homogeneity of Variance[/C][/ROW]
[ROW][C] [/C][C]Df[/C][C]F value[/C][C]Pr(>F)[/C][/ROW]
[ROW][C]Group[/C][C]5[/C][C]3.525[/C][C]0.006[/C][/ROW]
[ROW][C] [/C][C]84[/C][C] [/C][C] [/C][/ROW]
[/TABLE]
Source: https://freestatistics.org/blog/index.php?pk=136829&T=4

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=136829&T=4

As an alternative you can also use a QR Code:

The GUIDs for individual cells are displayed in the table below:

Levenes Test for Homogeneity of Variance
	Df	F value	Pr(>F)
Group	5	3.525	0.006
	84

Figure 1

PNG link

Postscript link

PDF link

Figure 2

PNG link

Postscript link

PDF link

Figure 3

PNG link

Postscript link

PDF link

Figure 4

PNG link

Postscript link

PDF link

Parameters (Session):

par1 = 2 ; par2 = 1 ; par3 = TRUE ;

Parameters (R input):

par1 = 2 ; par2 = 1 ; par3 = 3 ; par4 = TRUE ;

R code (references can be found in the software module):

cat1 <- as.numeric(par1) #
cat2<- as.numeric(par2) #
cat3 <- as.numeric(par3)
intercept<-as.logical(par4)
x <- t(x)
x1<-as.numeric(x[,cat1])
f1<-as.character(x[,cat2])
f2 <- as.character(x[,cat3])
xdf<-data.frame(x1,f1, f2)
(V1<-dimnames(y)[[1]][cat1])
(V2<-dimnames(y)[[1]][cat2])
(V3 <-dimnames(y)[[1]][cat3])
names(xdf)<-c('Response', 'Treatment_A', 'Treatment_B')
if(intercept == FALSE) (lmxdf<-lm(Response ~ Treatment_A * Treatment_B- 1, data = xdf) ) else (lmxdf<-lm(Response ~ Treatment_A * Treatment_B, data = xdf) )
(aov.xdf<-aov(lmxdf) )
(anova.xdf<-anova(lmxdf) )
load(file='createtable')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a,'ANOVA Model', length(lmxdf$coefficients)+1,TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, lmxdf$call['formula'],length(lmxdf$coefficients)+1,TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'means',,TRUE)
for(i in 1:length(lmxdf$coefficients)){
a<-table.element(a, round(lmxdf$coefficients[i], digits=3),,FALSE)
}
a<-table.row.end(a)
a<-table.end(a)
table.save(a,file='mytable.tab')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a,'ANOVA Statistics', 5+1,TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, ' ',,TRUE)
a<-table.element(a, 'Df',,FALSE)
a<-table.element(a, 'Sum Sq',,FALSE)
a<-table.element(a, 'Mean Sq',,FALSE)
a<-table.element(a, 'F value',,FALSE)
a<-table.element(a, 'Pr(>F)',,FALSE)
a<-table.row.end(a)
for(i in 1 : length(rownames(anova.xdf))-1){
a<-table.row.start(a)
a<-table.element(a,rownames(anova.xdf)[i] ,,TRUE)
a<-table.element(a, anova.xdf$Df[1],,FALSE)
a<-table.element(a, round(anova.xdf$'Sum Sq'[i], digits=3),,FALSE)
a<-table.element(a, round(anova.xdf$'Mean Sq'[i], digits=3),,FALSE)
a<-table.element(a, round(anova.xdf$'F value'[i], digits=3),,FALSE)
a<-table.element(a, round(anova.xdf$'Pr(>F)'[i], digits=3),,FALSE)
a<-table.row.end(a)
}
a<-table.row.start(a)
a<-table.element(a, 'Residuals',,TRUE)
a<-table.element(a, anova.xdf$'Df'[i+1],,FALSE)
a<-table.element(a, round(anova.xdf$'Sum Sq'[i+1], digits=3),,FALSE)
a<-table.element(a, round(anova.xdf$'Mean Sq'[i+1], digits=3),,FALSE)
a<-table.element(a, ' ',,FALSE)
a<-table.element(a, ' ',,FALSE)
a<-table.row.end(a)
a<-table.end(a)
table.save(a,file='mytable1.tab')
bitmap(file='anovaplot.png')
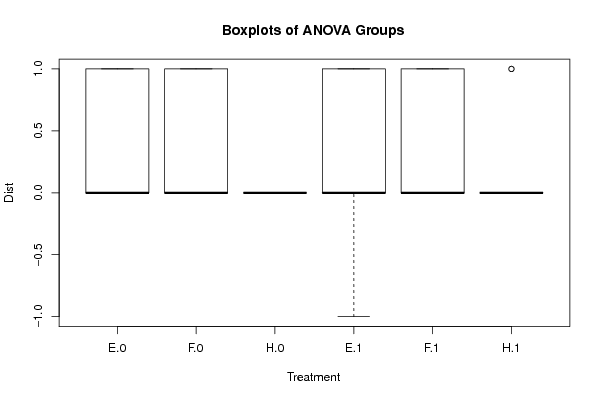
boxplot(Response ~ Treatment_A + Treatment_B, data=xdf, xlab=V2, ylab=V1, main='Boxplots of ANOVA Groups')
dev.off()
bitmap(file='designplot.png')
xdf2 <- xdf # to preserve xdf make copy for function
names(xdf2) <- c(V1, V2, V3)
plot.design(xdf2, main='Design Plot of Group Means')
dev.off()
bitmap(file='interactionplot.png')
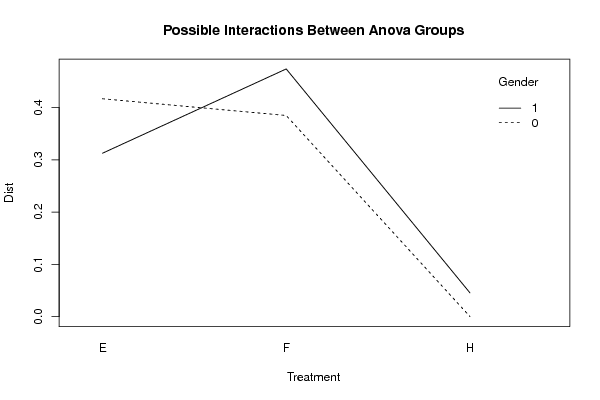
interaction.plot(xdf$Treatment_A, xdf$Treatment_B, xdf$Response, xlab=V2, ylab=V1, trace.label=V3, main='Possible Interactions Between Anova Groups')
dev.off()
if(intercept==TRUE){
thsd<-TukeyHSD(aov.xdf)
names(thsd) <- c(V2, V3, paste(V2, ':', V3, sep=''))
bitmap(file='TukeyHSDPlot.png')
layout(matrix(c(1,2,3,3), 2,2))
plot(thsd, las=1)
dev.off()
}
if(intercept==TRUE){
ntables<-length(names(thsd))
a<-table.start()
a<-table.row.start(a)
a<-table.element(a,'Tukey Honest Significant Difference Comparisons', 5,TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, ' ', 1, TRUE)
for(i in 1:4){
a<-table.element(a,colnames(thsd[[1]])[i], 1, TRUE)
}
a<-table.row.end(a)
for(nt in 1:ntables){
for(i in 1:length(rownames(thsd[[nt]]))){
a<-table.row.start(a)
a<-table.element(a,rownames(thsd[[nt]])[i], 1, TRUE)
for(j in 1:4){
a<-table.element(a,round(thsd[[nt]][i,j], digits=3), 1, FALSE)
}
a<-table.row.end(a)
}
} # end nt
a<-table.end(a)
table.save(a,file='hsdtable.tab')
}#end if hsd tables
if(intercept==FALSE){
a<-table.start()
a<-table.row.start(a)
a<-table.element(a,'TukeyHSD Message', 1,TRUE)
a<-table.row.end(a)
a<-table.start()
a<-table.row.start(a)
a<-table.element(a,'Must Include Intercept to use Tukey Test ', 1, FALSE)
a<-table.row.end(a)
a<-table.end(a)
table.save(a,file='mytable2.tab')
}
library(car)
lt.lmxdf<-levene.test(lmxdf)
a<-table.start()
a<-table.row.start(a)
a<-table.element(a,'Levenes Test for Homogeneity of Variance', 4,TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,' ', 1, TRUE)
for (i in 1:3){
a<-table.element(a,names(lt.lmxdf)[i], 1, FALSE)
}
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'Group', 1, TRUE)
for (i in 1:3){
a<-table.element(a,round(lt.lmxdf[[i]][1], digits=3), 1, FALSE)
}
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,' ', 1, TRUE)
a<-table.element(a,lt.lmxdf[[1]][2], 1, FALSE)
a<-table.element(a,' ', 1, FALSE)
a<-table.element(a,' ', 1, FALSE)
a<-table.row.end(a)
a<-table.end(a)
table.save(a,file='mytable3.tab')

Free Statistics

Description of Statistical Computation

Tree of Dependent Computations

Dataset

Tables (Output of Computation)

Figures (Output of Computation)

Input Parameters & R Code