| Multiple Linear Regression - Estimated Regression Equation |
| Som_Tevredenheid[t] = + 17.0083 + 0.249828IVHB1[t] -0.271285IVHB2[t] -0.254186IVHB3[t] + 0.120956`IVHB4\r`[t] + e[t] |
| Multiple Linear Regression - Ordinary Least Squares | |||||
| Variable | Parameter | S.D. | T-STAT H0: parameter = 0 | 2-tail p-value | 1-tail p-value |
| (Intercept) | +17.01 | 1.438 | +1.1830e+01 | 3.881e-23 | 1.94e-23 |
| IVHB1 | +0.2498 | 0.1903 | +1.3130e+00 | 0.1913 | 0.09567 |
| IVHB2 | -0.2713 | 0.1725 | -1.5730e+00 | 0.1179 | 0.05894 |
| IVHB3 | -0.2542 | 0.2013 | -1.2630e+00 | 0.2086 | 0.1043 |
| `IVHB4\r` | +0.121 | 0.2557 | +4.7290e-01 | 0.6369 | 0.3185 |
| Multiple Linear Regression - Regression Statistics | |
| Multiple R | 0.195 |
| R-squared | 0.03804 |
| Adjusted R-squared | 0.01204 |
| F-TEST (value) | 1.463 |
| F-TEST (DF numerator) | 4 |
| F-TEST (DF denominator) | 148 |
| p-value | 0.2163 |
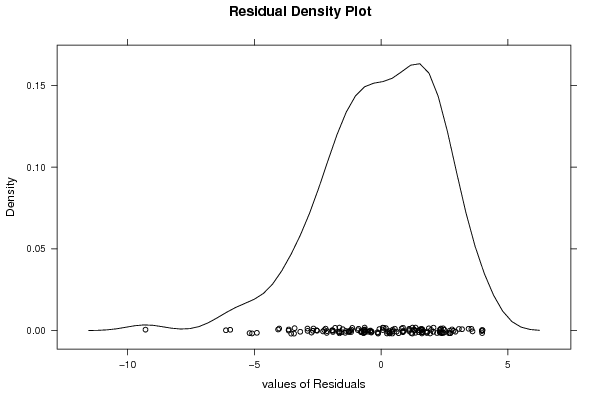
| Multiple Linear Regression - Residual Statistics | |
| Residual Standard Deviation | 2.332 |
| Sum Squared Residuals | 805 |
| Multiple Linear Regression - Actuals, Interpolation, and Residuals | |||
| Time or Index | Actuals | Interpolation Forecast | Residuals Prediction Error |
| 1 | 14 | 16.69 | -2.687 |
| 2 | 19 | 17.69 | 1.305 |
| 3 | 17 | 16.68 | 0.3221 |
| 4 | 17 | 16.66 | 0.3392 |
| 5 | 15 | 16.27 | -1.273 |
| 6 | 20 | 17.29 | 2.71 |
| 7 | 15 | 15.64 | -0.6401 |
| 8 | 19 | 16.68 | 2.322 |
| 9 | 15 | 16.64 | -1.644 |
| 10 | 19 | 16.94 | 2.059 |
| 11 | 20 | 16 | 4.003 |
| 12 | 18 | 16.64 | 1.361 |
| 13 | 15 | 16.93 | -1.932 |
| 14 | 14 | 15.66 | -1.657 |
| 15 | 20 | 17.33 | 2.667 |
| 16 | 16 | 17.17 | -1.169 |
| 17 | 16 | 16.64 | -0.6394 |
| 18 | 16 | 16.37 | -0.3681 |
| 19 | 10 | 16.12 | -6.118 |
| 20 | 19 | 16.2 | 2.8 |
| 21 | 19 | 16.64 | 2.356 |
| 22 | 16 | 16.43 | -0.4325 |
| 23 | 15 | 16.64 | -1.644 |
| 24 | 18 | 16.77 | 1.227 |
| 25 | 17 | 16.54 | 0.4558 |
| 26 | 19 | 16.51 | 2.494 |
| 27 | 17 | 16.68 | 0.3177 |
| 28 | 19 | 16.14 | 2.856 |
| 29 | 20 | 16.44 | 3.563 |
| 30 | 19 | 17.07 | 1.935 |
| 31 | 16 | 16.64 | -0.6437 |
| 32 | 15 | 16.67 | -1.665 |
| 33 | 16 | 16.78 | -0.7774 |
| 34 | 18 | 16.64 | 1.356 |
| 35 | 15 | 16.91 | -1.915 |
| 36 | 17 | 16.31 | 0.6885 |
| 37 | 20 | 17.07 | 2.934 |
| 38 | 19 | 16.68 | 2.318 |
| 39 | 7 | 16.29 | -9.29 |
| 40 | 13 | 16.54 | -3.544 |
| 41 | 16 | 16.39 | -0.3896 |
| 42 | 18 | 16.39 | 1.61 |
| 43 | 18 | 16.39 | 1.61 |
| 44 | 16 | 16.14 | -0.1441 |
| 45 | 17 | 17.69 | -0.6903 |
| 46 | 19 | 16.56 | 2.439 |
| 47 | 16 | 17.21 | -1.208 |
| 48 | 19 | 16.79 | 2.206 |
| 49 | 13 | 16.64 | -3.644 |
| 50 | 16 | 16.42 | -0.4189 |
| 51 | 13 | 16.41 | -3.411 |
| 52 | 12 | 17.19 | -5.186 |
| 53 | 17 | 16.66 | 0.3392 |
| 54 | 17 | 16.56 | 0.443 |
| 55 | 17 | 16.9 | 0.1021 |
| 56 | 16 | 16.79 | -0.7941 |
| 57 | 16 | 16.69 | -0.6867 |
| 58 | 14 | 16.52 | -2.523 |
| 59 | 16 | 16.12 | -0.1183 |
| 60 | 13 | 16.64 | -3.644 |
| 61 | 16 | 16.66 | -0.6608 |
| 62 | 14 | 17.19 | -3.186 |
| 63 | 20 | 17.55 | 2.448 |
| 64 | 12 | 16.02 | -4.019 |
| 65 | 13 | 15.9 | -2.902 |
| 66 | 18 | 16.9 | 1.102 |
| 67 | 14 | 16.74 | -2.743 |
| 68 | 19 | 16.64 | 2.356 |
| 69 | 18 | 16.76 | 1.24 |
| 70 | 14 | 16.14 | -2.143 |
| 71 | 18 | 16.42 | 1.585 |
| 72 | 19 | 16.93 | 2.068 |
| 73 | 15 | 16.9 | -1.898 |
| 74 | 14 | 16.9 | -2.898 |
| 75 | 17 | 16.77 | 0.2309 |
| 76 | 19 | 17.19 | 1.814 |
| 77 | 13 | 16.43 | -3.432 |
| 78 | 19 | 17.71 | 1.293 |
| 79 | 20 | 16.03 | 3.973 |
| 80 | 15 | 15.89 | -0.8899 |
| 81 | 15 | 16.64 | -1.644 |
| 82 | 15 | 16.29 | -1.29 |
| 83 | 20 | 16.39 | 3.606 |
| 84 | 15 | 16.14 | -1.135 |
| 85 | 19 | 16.27 | 2.731 |
| 86 | 18 | 16.81 | 1.189 |
| 87 | 18 | 16.39 | 1.606 |
| 88 | 15 | 16.51 | -1.511 |
| 89 | 20 | 17.6 | 2.405 |
| 90 | 17 | 16.14 | 0.8603 |
| 91 | 12 | 16.06 | -4.062 |
| 92 | 18 | 16.66 | 1.339 |
| 93 | 19 | 16.53 | 2.468 |
| 94 | 20 | 16.02 | 3.981 |
| 95 | 17 | 16.39 | 0.6148 |
| 96 | 16 | 16.51 | -0.5062 |
| 97 | 18 | 16.39 | 1.61 |
| 98 | 18 | 16.12 | 1.882 |
| 99 | 14 | 16.24 | -2.239 |
| 100 | 15 | 16.81 | -1.811 |
| 101 | 12 | 17.09 | -5.087 |
| 102 | 17 | 16.54 | 0.4601 |
| 103 | 14 | 16.67 | -2.665 |
| 104 | 18 | 17.46 | 0.5424 |
| 105 | 17 | 16.14 | 0.8559 |
| 106 | 17 | 15.89 | 1.106 |
| 107 | 20 | 17.69 | 2.31 |
| 108 | 16 | 16.39 | -0.3896 |
| 109 | 14 | 16.54 | -2.544 |
| 110 | 15 | 16.9 | -1.898 |
| 111 | 18 | 16.51 | 1.489 |
| 112 | 20 | 16.93 | 3.068 |
| 113 | 17 | 17.07 | -0.06536 |
| 114 | 17 | 15.89 | 1.11 |
| 115 | 17 | 16.14 | 0.8646 |
| 116 | 17 | 16.81 | 0.1888 |
| 117 | 17 | 16.93 | 0.06787 |
| 118 | 18 | 16.44 | 1.56 |
| 119 | 17 | 16.12 | 0.8817 |
| 120 | 20 | 16.81 | 3.193 |
| 121 | 16 | 17.18 | -1.182 |
| 122 | 15 | 16.39 | -1.39 |
| 123 | 18 | 15.61 | 2.386 |
| 124 | 15 | 15.65 | -0.648 |
| 125 | 18 | 16.03 | 1.972 |
| 126 | 20 | 16.55 | 3.451 |
| 127 | 19 | 17.2 | 1.797 |
| 128 | 14 | 16.14 | -2.135 |
| 129 | 16 | 16.62 | -0.6223 |
| 130 | 15 | 16.26 | -1.261 |
| 131 | 17 | 16.14 | 0.8603 |
| 132 | 18 | 16.37 | 1.628 |
| 133 | 20 | 16.01 | 3.986 |
| 134 | 17 | 15.5 | 1.499 |
| 135 | 18 | 16.37 | 1.628 |
| 136 | 15 | 17.29 | -2.29 |
| 137 | 16 | 16.12 | -0.1183 |
| 138 | 11 | 16.95 | -5.949 |
| 139 | 15 | 16.42 | -1.415 |
| 140 | 18 | 17.56 | 0.4429 |
| 141 | 17 | 16.93 | 0.06787 |
| 142 | 12 | 16.9 | -4.898 |
| 143 | 19 | 17.19 | 1.814 |
| 144 | 18 | 16.37 | 1.628 |
| 145 | 15 | 15.77 | -0.7689 |
| 146 | 17 | 16.75 | 0.248 |
| 147 | 19 | 16.29 | 2.71 |
| 148 | 18 | 17.19 | 0.8137 |
| 149 | 19 | 16.64 | 2.356 |
| 150 | 16 | 17.56 | -1.561 |
| 151 | 16 | 16.91 | -0.915 |
| 152 | 16 | 16.67 | -0.6652 |
| 153 | 14 | 16.19 | -2.186 |
| Goldfeld-Quandt test for Heteroskedasticity | |||
| p-values | Alternative Hypothesis | ||
| breakpoint index | greater | 2-sided | less |
| 8 | 0.221 | 0.442 | 0.779 |
| 9 | 0.3214 | 0.6427 | 0.6786 |
| 10 | 0.3287 | 0.6574 | 0.6713 |
| 11 | 0.6074 | 0.7852 | 0.3926 |
| 12 | 0.4994 | 0.9988 | 0.5006 |
| 13 | 0.5144 | 0.9713 | 0.4856 |
| 14 | 0.4151 | 0.8302 | 0.5849 |
| 15 | 0.434 | 0.8681 | 0.566 |
| 16 | 0.429 | 0.858 | 0.571 |
| 17 | 0.384 | 0.768 | 0.616 |
| 18 | 0.3189 | 0.6377 | 0.6811 |
| 19 | 0.6912 | 0.6175 | 0.3088 |
| 20 | 0.6857 | 0.6286 | 0.3143 |
| 21 | 0.6973 | 0.6053 | 0.3027 |
| 22 | 0.6386 | 0.7229 | 0.3614 |
| 23 | 0.5933 | 0.8134 | 0.4067 |
| 24 | 0.5321 | 0.9358 | 0.4679 |
| 25 | 0.4631 | 0.9263 | 0.5369 |
| 26 | 0.4817 | 0.9635 | 0.5183 |
| 27 | 0.4178 | 0.8356 | 0.5822 |
| 28 | 0.4839 | 0.9677 | 0.5161 |
| 29 | 0.5295 | 0.941 | 0.4705 |
| 30 | 0.4839 | 0.9679 | 0.5161 |
| 31 | 0.4283 | 0.8567 | 0.5717 |
| 32 | 0.4155 | 0.831 | 0.5845 |
| 33 | 0.3682 | 0.7363 | 0.6318 |
| 34 | 0.3303 | 0.6606 | 0.6697 |
| 35 | 0.3312 | 0.6623 | 0.6688 |
| 36 | 0.2814 | 0.5628 | 0.7186 |
| 37 | 0.2782 | 0.5563 | 0.7218 |
| 38 | 0.2627 | 0.5254 | 0.7373 |
| 39 | 0.9036 | 0.1928 | 0.09642 |
| 40 | 0.9178 | 0.1645 | 0.08225 |
| 41 | 0.8958 | 0.2084 | 0.1042 |
| 42 | 0.8848 | 0.2304 | 0.1152 |
| 43 | 0.8721 | 0.2558 | 0.1279 |
| 44 | 0.8427 | 0.3147 | 0.1573 |
| 45 | 0.8195 | 0.361 | 0.1805 |
| 46 | 0.8347 | 0.3305 | 0.1653 |
| 47 | 0.8207 | 0.3587 | 0.1793 |
| 48 | 0.8255 | 0.349 | 0.1745 |
| 49 | 0.8658 | 0.2685 | 0.1342 |
| 50 | 0.8401 | 0.3198 | 0.1599 |
| 51 | 0.8692 | 0.2616 | 0.1308 |
| 52 | 0.9474 | 0.1052 | 0.05258 |
| 53 | 0.9332 | 0.1337 | 0.06684 |
| 54 | 0.9175 | 0.1649 | 0.08247 |
| 55 | 0.8972 | 0.2056 | 0.1028 |
| 56 | 0.8755 | 0.249 | 0.1245 |
| 57 | 0.8523 | 0.2954 | 0.1477 |
| 58 | 0.8506 | 0.2987 | 0.1494 |
| 59 | 0.8219 | 0.3562 | 0.1781 |
| 60 | 0.8602 | 0.2797 | 0.1398 |
| 61 | 0.8336 | 0.3327 | 0.1664 |
| 62 | 0.8585 | 0.2831 | 0.1415 |
| 63 | 0.8627 | 0.2746 | 0.1373 |
| 64 | 0.8992 | 0.2017 | 0.1008 |
| 65 | 0.9048 | 0.1905 | 0.09524 |
| 66 | 0.8877 | 0.2246 | 0.1123 |
| 67 | 0.8999 | 0.2002 | 0.1001 |
| 68 | 0.9013 | 0.1974 | 0.09871 |
| 69 | 0.8844 | 0.2312 | 0.1156 |
| 70 | 0.8906 | 0.2188 | 0.1094 |
| 71 | 0.8818 | 0.2363 | 0.1182 |
| 72 | 0.8774 | 0.2452 | 0.1226 |
| 73 | 0.8727 | 0.2547 | 0.1273 |
| 74 | 0.893 | 0.2139 | 0.107 |
| 75 | 0.8699 | 0.2602 | 0.1301 |
| 76 | 0.8595 | 0.281 | 0.1405 |
| 77 | 0.8813 | 0.2373 | 0.1187 |
| 78 | 0.8641 | 0.2717 | 0.1359 |
| 79 | 0.9116 | 0.1768 | 0.0884 |
| 80 | 0.8935 | 0.2129 | 0.1065 |
| 81 | 0.8851 | 0.2298 | 0.1149 |
| 82 | 0.8695 | 0.2609 | 0.1305 |
| 83 | 0.9037 | 0.1927 | 0.09634 |
| 84 | 0.8895 | 0.2209 | 0.1105 |
| 85 | 0.895 | 0.2099 | 0.105 |
| 86 | 0.8769 | 0.2462 | 0.1231 |
| 87 | 0.864 | 0.2721 | 0.136 |
| 88 | 0.8486 | 0.3028 | 0.1514 |
| 89 | 0.8644 | 0.2711 | 0.1356 |
| 90 | 0.8409 | 0.3183 | 0.1591 |
| 91 | 0.8887 | 0.2226 | 0.1113 |
| 92 | 0.8718 | 0.2563 | 0.1282 |
| 93 | 0.8787 | 0.2426 | 0.1213 |
| 94 | 0.9179 | 0.1643 | 0.08215 |
| 95 | 0.8985 | 0.203 | 0.1015 |
| 96 | 0.8784 | 0.2431 | 0.1216 |
| 97 | 0.8623 | 0.2754 | 0.1377 |
| 98 | 0.8481 | 0.3039 | 0.1519 |
| 99 | 0.8572 | 0.2857 | 0.1428 |
| 100 | 0.846 | 0.3079 | 0.154 |
| 101 | 0.9289 | 0.1423 | 0.07114 |
| 102 | 0.91 | 0.18 | 0.08999 |
| 103 | 0.9183 | 0.1634 | 0.08172 |
| 104 | 0.8992 | 0.2016 | 0.1008 |
| 105 | 0.8769 | 0.2461 | 0.1231 |
| 106 | 0.8551 | 0.2898 | 0.1449 |
| 107 | 0.8657 | 0.2685 | 0.1343 |
| 108 | 0.8378 | 0.3243 | 0.1622 |
| 109 | 0.8494 | 0.3011 | 0.1506 |
| 110 | 0.8401 | 0.3199 | 0.1599 |
| 111 | 0.8184 | 0.3632 | 0.1816 |
| 112 | 0.8524 | 0.2953 | 0.1476 |
| 113 | 0.8174 | 0.3653 | 0.1826 |
| 114 | 0.7838 | 0.4324 | 0.2162 |
| 115 | 0.743 | 0.514 | 0.257 |
| 116 | 0.6943 | 0.6113 | 0.3057 |
| 117 | 0.6425 | 0.715 | 0.3575 |
| 118 | 0.6031 | 0.7937 | 0.3969 |
| 119 | 0.5484 | 0.9031 | 0.4516 |
| 120 | 0.6115 | 0.7769 | 0.3885 |
| 121 | 0.5578 | 0.8845 | 0.4422 |
| 122 | 0.523 | 0.9539 | 0.477 |
| 123 | 0.5015 | 0.997 | 0.4985 |
| 124 | 0.4724 | 0.9449 | 0.5276 |
| 125 | 0.5074 | 0.9852 | 0.4926 |
| 126 | 0.5555 | 0.889 | 0.4445 |
| 127 | 0.5998 | 0.8004 | 0.4002 |
| 128 | 0.5978 | 0.8044 | 0.4022 |
| 129 | 0.5834 | 0.8331 | 0.4166 |
| 130 | 0.5301 | 0.9398 | 0.4699 |
| 131 | 0.4629 | 0.9258 | 0.5371 |
| 132 | 0.3964 | 0.7928 | 0.6036 |
| 133 | 0.4753 | 0.9506 | 0.5247 |
| 134 | 0.4063 | 0.8126 | 0.5937 |
| 135 | 0.3412 | 0.6824 | 0.6588 |
| 136 | 0.305 | 0.61 | 0.695 |
| 137 | 0.2379 | 0.4758 | 0.7621 |
| 138 | 0.6819 | 0.6362 | 0.3181 |
| 139 | 0.6136 | 0.7727 | 0.3864 |
| 140 | 0.5415 | 0.917 | 0.4585 |
| 141 | 0.5794 | 0.8412 | 0.4206 |
| 142 | 0.7372 | 0.5256 | 0.2628 |
| 143 | 0.7207 | 0.5586 | 0.2793 |
| 144 | 0.6193 | 0.7614 | 0.3807 |
| 145 | 0.5029 | 0.9942 | 0.4971 |
| Meta Analysis of Goldfeld-Quandt test for Heteroskedasticity | |||
| Description | # significant tests | % significant tests | OK/NOK |
| 1% type I error level | 0 | 0 | OK |
| 5% type I error level | 0 | 0 | OK |
| 10% type I error level | 0 | 0 | OK |
| Ramsey RESET F-Test for powers (2 and 3) of fitted values |
> reset_test_fitted RESET test data: mylm RESET = 1.2518, df1 = 2, df2 = 146, p-value = 0.289 |
| Ramsey RESET F-Test for powers (2 and 3) of regressors |
> reset_test_regressors RESET test data: mylm RESET = 0.90468, df1 = 8, df2 = 140, p-value = 0.5145 |
| Ramsey RESET F-Test for powers (2 and 3) of principal components |
> reset_test_principal_components RESET test data: mylm RESET = 2.1469, df1 = 2, df2 = 146, p-value = 0.1205 |
| Variance Inflation Factors (Multicollinearity) |
> vif
IVHB1 IVHB2 IVHB3 `IVHB4\\r`
1.038729 1.038396 1.044089 1.042759
|