Repository of Reproducible Computations

Free Statistics

of Irreproducible Research!

Author's title

Author

*The author of this computation has been verified*

R Software Module

rwasp_multipleregression.wasp

Title produced by software

Multiple Regression

Date of computation

Wed, 10 Dec 2014 15:09:31 +0000

Cite this page as follows

Statistical Computations at FreeStatistics.org, Office for Research Development and Education, URL https://freestatistics.org/blog/index.php?v=date/2014/Dec/10/t1418224902vlikc4ik4skpdot.htm/, Retrieved Sun, 04 May 2025 23:51:13 +0000

Statistical Computations at FreeStatistics.org, Office for Research Development and Education, URL https://freestatistics.org/blog/index.php?pk=265361, Retrieved Sun, 04 May 2025 23:51:13 +0000

QR Codes:

Paste this QR Code to cite your computation.

Original text written by user:

IsPrivate?

No (this computation is public)

User-defined keywords

Estimated Impact

153

Family? (F = Feedback message, R = changed R code, M = changed R Module, P = changed Parameters, D = changed Data)

-       [Multiple Regression] [] [2014-12-10 15:09:31] [20f13859937b25726fc27e6925bc2ae4] [Current]
- RM      [Multiple Regression] [] [2014-12-12 13:22:41] [93cb0d178904cf975da218b7c929e42d] 
- RMPD    [Skewness and Kurtosis Test] [] [2014-12-17 13:02:38] [93cb0d178904cf975da218b7c929e42d] 
- RMPD    [Central Tendency] [] [2014-12-17 13:21:46] [93cb0d178904cf975da218b7c929e42d] 
- RMPD    [Two-Way ANOVA] [] [2014-12-17 13:33:51] [93cb0d178904cf975da218b7c929e42d] 

Feedback Forum

Post a new message

Dataseries X:

Download CSV

Histogram

Boxplots

7.5 12 13 13
6.5 11 11 11
1.0 13 14 10
1.0 11 15 9
5.5 10 14 8
8.5 7 11 26
6.5 10 13 10
4.5 15 16 10
2.0 12 14 8
5.0 12 14 13
0.5 10 15 11
5.0 14 13 12
2.5 6 14 24
5.0 12 11 21
5.5 14 12 5
3.5 11 14 14
4.0 12 12 9
6.5 13 15 17
4.5 11 14 18
5.5 7 12 23
4.0 11 12 9
7.5 7 12 14
4.0 12 14 10
5.5 13 16 8
2.5 9 12 10
5.5 11 12 19
3.5 12 14 11
4.5 12 15 12
4.5 5 14 11
6.0 13 13 10
5.0 6 16 14
6.5 6 15 11
5.0 12 13 13
6.0 11 16 15
4.5 6 16 15
5.0 11 15 14
5.0 12 13 12
6.5 13 12 13
7.0 14 14 7
4.5 12 14 8
8.5 14 10 20
3.5 11 16 16
6.0 10 14 11
1.5 7 14 26
3.5 7 15 15
7.5 10 16 20
5.0 12 15 15
6.5 5 13 17
6.5 10 12 19
6.5 12 12 13
7.0 11 14 8
1.5 12 15 9
4.0 11 11 12
4.5 12 14 9
0.0 10 16 14
3.5 9 13 14
4.5 7 11 13
0.0 9 12 16
3.0 10 12 14
3.5 12 14 11
3.0 14 12 11
1.0 9 13 14
5.5 12 14 15

Summary of computational transaction
Raw Input	view raw input (R code)
Raw Output	view raw output of R engine
Computing time	5 seconds
R Server	'Gwilym Jenkins' @ jenkins.wessa.net

\begin{tabular}{lllllllll}
\hline
Summary of computational transaction \tabularnewline
Raw Input & view raw input (R code)  \tabularnewline
Raw Output & view raw output of R engine  \tabularnewline
Computing time & 5 seconds \tabularnewline
R Server & 'Gwilym Jenkins' @ jenkins.wessa.net \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=265361&T=0

[TABLE]
[ROW][C]Summary of computational transaction[/C][/ROW]
[ROW][C]Raw Input[/C][C]view raw input (R code) [/C][/ROW]
[ROW][C]Raw Output[/C][C]view raw output of R engine [/C][/ROW]
[ROW][C]Computing time[/C][C]5 seconds[/C][/ROW]
[ROW][C]R Server[/C][C]'Gwilym Jenkins' @ jenkins.wessa.net[/C][/ROW]
[/TABLE]
Source: https://freestatistics.org/blog/index.php?pk=265361&T=0

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=265361&T=0

As an alternative you can also use a QR Code:

The GUIDs for individual cells are displayed in the table below:

Summary of computational transaction
Raw Input	view raw input (R code)
Raw Output	view raw output of R engine
Computing time	5 seconds
R Server	'Gwilym Jenkins' @ jenkins.wessa.net

Multiple Linear Regression - Estimated Regression Equation
Ex[t] = + 6.27376 + 0.0984574Conf[t] -0.26679Stress[t] + 0.0662546Dep[t] + e[t]

\begin{tabular}{lllllllll}
\hline
Multiple Linear Regression - Estimated Regression Equation \tabularnewline
Ex[t] =  +  6.27376 +  0.0984574Conf[t] -0.26679Stress[t] +  0.0662546Dep[t]  + e[t] \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=265361&T=1

[TABLE]
[ROW][C]Multiple Linear Regression - Estimated Regression Equation[/C][/ROW]
[ROW][C]Ex[t] =  +  6.27376 +  0.0984574Conf[t] -0.26679Stress[t] +  0.0662546Dep[t]  + e[t][/C][/ROW]
[/TABLE]
Source: https://freestatistics.org/blog/index.php?pk=265361&T=1

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=265361&T=1

As an alternative you can also use a QR Code:

The GUIDs for individual cells are displayed in the table below:

Multiple Linear Regression - Estimated Regression Equation
Ex[t] = + 6.27376 + 0.0984574Conf[t] -0.26679Stress[t] + 0.0662546Dep[t] + e[t]

Multiple Linear Regression - Ordinary Least Squares
Variable	Parameter	S.D.	T-STATH0: parameter = 0	2-tail p-value	1-tail p-value
(Intercept)	6.27376	3.10663	2.019	0.0479879	0.023994
Conf	0.0984574	0.114635	0.8589	0.393885	0.196942
Stress	-0.26679	0.166765	-1.6	0.114986	0.0574931
Dep	0.0662546	0.0630761	1.05	0.297822	0.148911

\begin{tabular}{lllllllll}
\hline
Multiple Linear Regression - Ordinary Least Squares \tabularnewline
Variable & Parameter & S.D. & T-STATH0: parameter = 0 & 2-tail p-value & 1-tail p-value \tabularnewline
(Intercept) & 6.27376 & 3.10663 & 2.019 & 0.0479879 & 0.023994 \tabularnewline
Conf & 0.0984574 & 0.114635 & 0.8589 & 0.393885 & 0.196942 \tabularnewline
Stress & -0.26679 & 0.166765 & -1.6 & 0.114986 & 0.0574931 \tabularnewline
Dep & 0.0662546 & 0.0630761 & 1.05 & 0.297822 & 0.148911 \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=265361&T=2

[TABLE]
[ROW][C]Multiple Linear Regression - Ordinary Least Squares[/C][/ROW]
[ROW][C]Variable[/C][C]Parameter[/C][C]S.D.[/C][C]T-STATH0: parameter = 0[/C][C]2-tail p-value[/C][C]1-tail p-value[/C][/ROW]
[ROW][C](Intercept)[/C][C]6.27376[/C][C]3.10663[/C][C]2.019[/C][C]0.0479879[/C][C]0.023994[/C][/ROW]
[ROW][C]Conf[/C][C]0.0984574[/C][C]0.114635[/C][C]0.8589[/C][C]0.393885[/C][C]0.196942[/C][/ROW]
[ROW][C]Stress[/C][C]-0.26679[/C][C]0.166765[/C][C]-1.6[/C][C]0.114986[/C][C]0.0574931[/C][/ROW]
[ROW][C]Dep[/C][C]0.0662546[/C][C]0.0630761[/C][C]1.05[/C][C]0.297822[/C][C]0.148911[/C][/ROW]
[/TABLE]
Source: https://freestatistics.org/blog/index.php?pk=265361&T=2

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=265361&T=2

As an alternative you can also use a QR Code:

The GUIDs for individual cells are displayed in the table below:

Multiple Linear Regression - Ordinary Least Squares
Variable	Parameter	S.D.	T-STATH0: parameter = 0	2-tail p-value	1-tail p-value
(Intercept)	6.27376	3.10663	2.019	0.0479879	0.023994
Conf	0.0984574	0.114635	0.8589	0.393885	0.196942
Stress	-0.26679	0.166765	-1.6	0.114986	0.0574931
Dep	0.0662546	0.0630761	1.05	0.297822	0.148911

Multiple Linear Regression - Regression Statistics
Multiple R	0.273022
R-squared	0.0745412
Adjusted R-squared	0.027484
F-TEST (value)	1.58405
F-TEST (DF numerator)	3
F-TEST (DF denominator)	59
p-value	0.202798
Multiple Linear Regression - Residual Statistics
Residual Standard Deviation	1.99906
Sum Squared Residuals	235.779

\begin{tabular}{lllllllll}
\hline
Multiple Linear Regression - Regression Statistics \tabularnewline
Multiple R & 0.273022 \tabularnewline
R-squared & 0.0745412 \tabularnewline
Adjusted R-squared & 0.027484 \tabularnewline
F-TEST (value) & 1.58405 \tabularnewline
F-TEST (DF numerator) & 3 \tabularnewline
F-TEST (DF denominator) & 59 \tabularnewline
p-value & 0.202798 \tabularnewline
Multiple Linear Regression - Residual Statistics \tabularnewline
Residual Standard Deviation & 1.99906 \tabularnewline
Sum Squared Residuals & 235.779 \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=265361&T=3

[TABLE]
[ROW][C]Multiple Linear Regression - Regression Statistics[/C][/ROW]
[ROW][C]Multiple R[/C][C]0.273022[/C][/ROW]
[ROW][C]R-squared[/C][C]0.0745412[/C][/ROW]
[ROW][C]Adjusted R-squared[/C][C]0.027484[/C][/ROW]
[ROW][C]F-TEST (value)[/C][C]1.58405[/C][/ROW]
[ROW][C]F-TEST (DF numerator)[/C][C]3[/C][/ROW]
[ROW][C]F-TEST (DF denominator)[/C][C]59[/C][/ROW]
[ROW][C]p-value[/C][C]0.202798[/C][/ROW]
[ROW][C]Multiple Linear Regression - Residual Statistics[/C][/ROW]
[ROW][C]Residual Standard Deviation[/C][C]1.99906[/C][/ROW]
[ROW][C]Sum Squared Residuals[/C][C]235.779[/C][/ROW]
[/TABLE]
Source: https://freestatistics.org/blog/index.php?pk=265361&T=3

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=265361&T=3

As an alternative you can also use a QR Code:

The GUIDs for individual cells are displayed in the table below:

Multiple Linear Regression - Regression Statistics
Multiple R	0.273022
R-squared	0.0745412
Adjusted R-squared	0.027484
F-TEST (value)	1.58405
F-TEST (DF numerator)	3
F-TEST (DF denominator)	59
p-value	0.202798
Multiple Linear Regression - Residual Statistics
Residual Standard Deviation	1.99906
Sum Squared Residuals	235.779

Multiple Linear Regression - Actuals, Interpolation, and Residuals
Time or Index	Actuals	InterpolationForecast	ResidualsPrediction Error
1	7.5	4.84829	2.65171
2	6.5	5.1509	1.3491
3	1	4.48119	-3.48119
4	1	3.95123	-2.95123
5	5.5	4.05331	1.44669
6	8.5	5.75089	2.74911
7	6.5	4.45261	2.04739
8	4.5	4.14453	0.355473
9	2	4.25023	-2.25023
10	5	4.5815	0.418501
11	0.5	3.98529	-3.48529
12	5	4.97895	0.0210505
13	2.5	4.71956	-2.21956
14	5	5.91191	-0.911906
15	5.5	4.78196	0.718043
16	3.5	4.5493	-1.0493
17	4	4.85006	-0.850061
18	6.5	4.67818	1.82182
19	4.5	4.81431	-0.314315
20	5.5	5.28534	0.214661
21	4	4.7516	-0.751604
22	7.5	4.68905	2.81095
23	4	4.38274	-0.382735
24	5.5	3.8151	1.6849
25	2.5	4.62094	-2.12094
26	5.5	5.41415	0.0858503
27	3.5	4.44899	-0.94899
28	4.5	4.24845	0.251546
29	4.5	3.75979	0.740212
30	6	4.74798	1.25202
31	5	3.52343	1.47657
32	6.5	3.59146	2.90854
33	5	4.84829	0.151711
34	6	4.08197	1.91803
35	4.5	3.58968	0.910316
36	5	4.28251	0.717494
37	5	4.78203	0.217965
38	6.5	5.21354	1.28646
39	7	4.38089	2.61911
40	4.5	4.25023	0.249774
41	8.5	6.30936	2.19064
42	3.5	4.14823	-0.648225
43	6	4.25208	1.74792
44	1.5	4.95052	-3.45052
45	3.5	3.95493	-0.454931
46	7.5	4.31479	3.18521
47	5	4.44722	0.552782
48	6.5	4.42411	2.07589
49	6.5	5.31569	1.18431
50	6.5	5.11508	1.38492
51	7	4.15177	2.84823
52	1.5	4.04969	-2.54969
53	4	5.21716	-1.21716
54	4.5	4.31648	0.183519
55	0	3.91726	-3.91726
56	3.5	4.61917	-1.11917
57	4.5	4.88958	-0.389583
58	0	5.01847	-5.01847
59	3	4.98442	-1.98442
60	3.5	4.44899	-0.94899
61	3	5.17949	-2.17949
62	1	4.61917	-3.61917
63	5.5	4.71401	0.785992

\begin{tabular}{lllllllll}
\hline
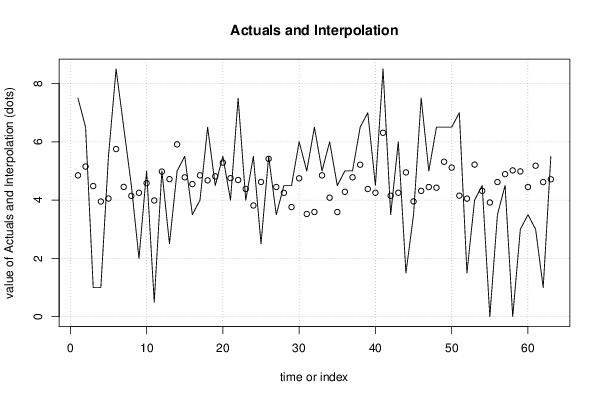
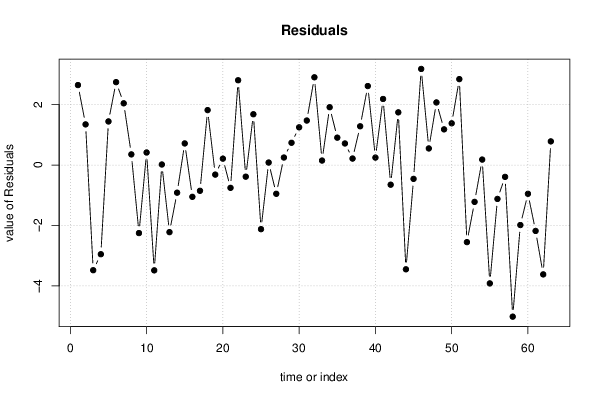
Multiple Linear Regression - Actuals, Interpolation, and Residuals \tabularnewline
Time or Index & Actuals & InterpolationForecast & ResidualsPrediction Error \tabularnewline
1 & 7.5 & 4.84829 & 2.65171 \tabularnewline
2 & 6.5 & 5.1509 & 1.3491 \tabularnewline
3 & 1 & 4.48119 & -3.48119 \tabularnewline
4 & 1 & 3.95123 & -2.95123 \tabularnewline
5 & 5.5 & 4.05331 & 1.44669 \tabularnewline
6 & 8.5 & 5.75089 & 2.74911 \tabularnewline
7 & 6.5 & 4.45261 & 2.04739 \tabularnewline
8 & 4.5 & 4.14453 & 0.355473 \tabularnewline
9 & 2 & 4.25023 & -2.25023 \tabularnewline
10 & 5 & 4.5815 & 0.418501 \tabularnewline
11 & 0.5 & 3.98529 & -3.48529 \tabularnewline
12 & 5 & 4.97895 & 0.0210505 \tabularnewline
13 & 2.5 & 4.71956 & -2.21956 \tabularnewline
14 & 5 & 5.91191 & -0.911906 \tabularnewline
15 & 5.5 & 4.78196 & 0.718043 \tabularnewline
16 & 3.5 & 4.5493 & -1.0493 \tabularnewline
17 & 4 & 4.85006 & -0.850061 \tabularnewline
18 & 6.5 & 4.67818 & 1.82182 \tabularnewline
19 & 4.5 & 4.81431 & -0.314315 \tabularnewline
20 & 5.5 & 5.28534 & 0.214661 \tabularnewline
21 & 4 & 4.7516 & -0.751604 \tabularnewline
22 & 7.5 & 4.68905 & 2.81095 \tabularnewline
23 & 4 & 4.38274 & -0.382735 \tabularnewline
24 & 5.5 & 3.8151 & 1.6849 \tabularnewline
25 & 2.5 & 4.62094 & -2.12094 \tabularnewline
26 & 5.5 & 5.41415 & 0.0858503 \tabularnewline
27 & 3.5 & 4.44899 & -0.94899 \tabularnewline
28 & 4.5 & 4.24845 & 0.251546 \tabularnewline
29 & 4.5 & 3.75979 & 0.740212 \tabularnewline
30 & 6 & 4.74798 & 1.25202 \tabularnewline
31 & 5 & 3.52343 & 1.47657 \tabularnewline
32 & 6.5 & 3.59146 & 2.90854 \tabularnewline
33 & 5 & 4.84829 & 0.151711 \tabularnewline
34 & 6 & 4.08197 & 1.91803 \tabularnewline
35 & 4.5 & 3.58968 & 0.910316 \tabularnewline
36 & 5 & 4.28251 & 0.717494 \tabularnewline
37 & 5 & 4.78203 & 0.217965 \tabularnewline
38 & 6.5 & 5.21354 & 1.28646 \tabularnewline
39 & 7 & 4.38089 & 2.61911 \tabularnewline
40 & 4.5 & 4.25023 & 0.249774 \tabularnewline
41 & 8.5 & 6.30936 & 2.19064 \tabularnewline
42 & 3.5 & 4.14823 & -0.648225 \tabularnewline
43 & 6 & 4.25208 & 1.74792 \tabularnewline
44 & 1.5 & 4.95052 & -3.45052 \tabularnewline
45 & 3.5 & 3.95493 & -0.454931 \tabularnewline
46 & 7.5 & 4.31479 & 3.18521 \tabularnewline
47 & 5 & 4.44722 & 0.552782 \tabularnewline
48 & 6.5 & 4.42411 & 2.07589 \tabularnewline
49 & 6.5 & 5.31569 & 1.18431 \tabularnewline
50 & 6.5 & 5.11508 & 1.38492 \tabularnewline
51 & 7 & 4.15177 & 2.84823 \tabularnewline
52 & 1.5 & 4.04969 & -2.54969 \tabularnewline
53 & 4 & 5.21716 & -1.21716 \tabularnewline
54 & 4.5 & 4.31648 & 0.183519 \tabularnewline
55 & 0 & 3.91726 & -3.91726 \tabularnewline
56 & 3.5 & 4.61917 & -1.11917 \tabularnewline
57 & 4.5 & 4.88958 & -0.389583 \tabularnewline
58 & 0 & 5.01847 & -5.01847 \tabularnewline
59 & 3 & 4.98442 & -1.98442 \tabularnewline
60 & 3.5 & 4.44899 & -0.94899 \tabularnewline
61 & 3 & 5.17949 & -2.17949 \tabularnewline
62 & 1 & 4.61917 & -3.61917 \tabularnewline
63 & 5.5 & 4.71401 & 0.785992 \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=265361&T=4

[TABLE]
[ROW][C]Multiple Linear Regression - Actuals, Interpolation, and Residuals[/C][/ROW]
[ROW][C]Time or Index[/C][C]Actuals[/C][C]InterpolationForecast[/C][C]ResidualsPrediction Error[/C][/ROW]
[ROW][C]1[/C][C]7.5[/C][C]4.84829[/C][C]2.65171[/C][/ROW]
[ROW][C]2[/C][C]6.5[/C][C]5.1509[/C][C]1.3491[/C][/ROW]
[ROW][C]3[/C][C]1[/C][C]4.48119[/C][C]-3.48119[/C][/ROW]
[ROW][C]4[/C][C]1[/C][C]3.95123[/C][C]-2.95123[/C][/ROW]
[ROW][C]5[/C][C]5.5[/C][C]4.05331[/C][C]1.44669[/C][/ROW]
[ROW][C]6[/C][C]8.5[/C][C]5.75089[/C][C]2.74911[/C][/ROW]
[ROW][C]7[/C][C]6.5[/C][C]4.45261[/C][C]2.04739[/C][/ROW]
[ROW][C]8[/C][C]4.5[/C][C]4.14453[/C][C]0.355473[/C][/ROW]
[ROW][C]9[/C][C]2[/C][C]4.25023[/C][C]-2.25023[/C][/ROW]
[ROW][C]10[/C][C]5[/C][C]4.5815[/C][C]0.418501[/C][/ROW]
[ROW][C]11[/C][C]0.5[/C][C]3.98529[/C][C]-3.48529[/C][/ROW]
[ROW][C]12[/C][C]5[/C][C]4.97895[/C][C]0.0210505[/C][/ROW]
[ROW][C]13[/C][C]2.5[/C][C]4.71956[/C][C]-2.21956[/C][/ROW]
[ROW][C]14[/C][C]5[/C][C]5.91191[/C][C]-0.911906[/C][/ROW]
[ROW][C]15[/C][C]5.5[/C][C]4.78196[/C][C]0.718043[/C][/ROW]
[ROW][C]16[/C][C]3.5[/C][C]4.5493[/C][C]-1.0493[/C][/ROW]
[ROW][C]17[/C][C]4[/C][C]4.85006[/C][C]-0.850061[/C][/ROW]
[ROW][C]18[/C][C]6.5[/C][C]4.67818[/C][C]1.82182[/C][/ROW]
[ROW][C]19[/C][C]4.5[/C][C]4.81431[/C][C]-0.314315[/C][/ROW]
[ROW][C]20[/C][C]5.5[/C][C]5.28534[/C][C]0.214661[/C][/ROW]
[ROW][C]21[/C][C]4[/C][C]4.7516[/C][C]-0.751604[/C][/ROW]
[ROW][C]22[/C][C]7.5[/C][C]4.68905[/C][C]2.81095[/C][/ROW]
[ROW][C]23[/C][C]4[/C][C]4.38274[/C][C]-0.382735[/C][/ROW]
[ROW][C]24[/C][C]5.5[/C][C]3.8151[/C][C]1.6849[/C][/ROW]
[ROW][C]25[/C][C]2.5[/C][C]4.62094[/C][C]-2.12094[/C][/ROW]
[ROW][C]26[/C][C]5.5[/C][C]5.41415[/C][C]0.0858503[/C][/ROW]
[ROW][C]27[/C][C]3.5[/C][C]4.44899[/C][C]-0.94899[/C][/ROW]
[ROW][C]28[/C][C]4.5[/C][C]4.24845[/C][C]0.251546[/C][/ROW]
[ROW][C]29[/C][C]4.5[/C][C]3.75979[/C][C]0.740212[/C][/ROW]
[ROW][C]30[/C][C]6[/C][C]4.74798[/C][C]1.25202[/C][/ROW]
[ROW][C]31[/C][C]5[/C][C]3.52343[/C][C]1.47657[/C][/ROW]
[ROW][C]32[/C][C]6.5[/C][C]3.59146[/C][C]2.90854[/C][/ROW]
[ROW][C]33[/C][C]5[/C][C]4.84829[/C][C]0.151711[/C][/ROW]
[ROW][C]34[/C][C]6[/C][C]4.08197[/C][C]1.91803[/C][/ROW]
[ROW][C]35[/C][C]4.5[/C][C]3.58968[/C][C]0.910316[/C][/ROW]
[ROW][C]36[/C][C]5[/C][C]4.28251[/C][C]0.717494[/C][/ROW]
[ROW][C]37[/C][C]5[/C][C]4.78203[/C][C]0.217965[/C][/ROW]
[ROW][C]38[/C][C]6.5[/C][C]5.21354[/C][C]1.28646[/C][/ROW]
[ROW][C]39[/C][C]7[/C][C]4.38089[/C][C]2.61911[/C][/ROW]
[ROW][C]40[/C][C]4.5[/C][C]4.25023[/C][C]0.249774[/C][/ROW]
[ROW][C]41[/C][C]8.5[/C][C]6.30936[/C][C]2.19064[/C][/ROW]
[ROW][C]42[/C][C]3.5[/C][C]4.14823[/C][C]-0.648225[/C][/ROW]
[ROW][C]43[/C][C]6[/C][C]4.25208[/C][C]1.74792[/C][/ROW]
[ROW][C]44[/C][C]1.5[/C][C]4.95052[/C][C]-3.45052[/C][/ROW]
[ROW][C]45[/C][C]3.5[/C][C]3.95493[/C][C]-0.454931[/C][/ROW]
[ROW][C]46[/C][C]7.5[/C][C]4.31479[/C][C]3.18521[/C][/ROW]
[ROW][C]47[/C][C]5[/C][C]4.44722[/C][C]0.552782[/C][/ROW]
[ROW][C]48[/C][C]6.5[/C][C]4.42411[/C][C]2.07589[/C][/ROW]
[ROW][C]49[/C][C]6.5[/C][C]5.31569[/C][C]1.18431[/C][/ROW]
[ROW][C]50[/C][C]6.5[/C][C]5.11508[/C][C]1.38492[/C][/ROW]
[ROW][C]51[/C][C]7[/C][C]4.15177[/C][C]2.84823[/C][/ROW]
[ROW][C]52[/C][C]1.5[/C][C]4.04969[/C][C]-2.54969[/C][/ROW]
[ROW][C]53[/C][C]4[/C][C]5.21716[/C][C]-1.21716[/C][/ROW]
[ROW][C]54[/C][C]4.5[/C][C]4.31648[/C][C]0.183519[/C][/ROW]
[ROW][C]55[/C][C]0[/C][C]3.91726[/C][C]-3.91726[/C][/ROW]
[ROW][C]56[/C][C]3.5[/C][C]4.61917[/C][C]-1.11917[/C][/ROW]
[ROW][C]57[/C][C]4.5[/C][C]4.88958[/C][C]-0.389583[/C][/ROW]
[ROW][C]58[/C][C]0[/C][C]5.01847[/C][C]-5.01847[/C][/ROW]
[ROW][C]59[/C][C]3[/C][C]4.98442[/C][C]-1.98442[/C][/ROW]
[ROW][C]60[/C][C]3.5[/C][C]4.44899[/C][C]-0.94899[/C][/ROW]
[ROW][C]61[/C][C]3[/C][C]5.17949[/C][C]-2.17949[/C][/ROW]
[ROW][C]62[/C][C]1[/C][C]4.61917[/C][C]-3.61917[/C][/ROW]
[ROW][C]63[/C][C]5.5[/C][C]4.71401[/C][C]0.785992[/C][/ROW]
[/TABLE]
Source: https://freestatistics.org/blog/index.php?pk=265361&T=4

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=265361&T=4

As an alternative you can also use a QR Code:

The GUIDs for individual cells are displayed in the table below:

Multiple Linear Regression - Actuals, Interpolation, and Residuals
Time or Index	Actuals	InterpolationForecast	ResidualsPrediction Error
1	7.5	4.84829	2.65171
2	6.5	5.1509	1.3491
3	1	4.48119	-3.48119
4	1	3.95123	-2.95123
5	5.5	4.05331	1.44669
6	8.5	5.75089	2.74911
7	6.5	4.45261	2.04739
8	4.5	4.14453	0.355473
9	2	4.25023	-2.25023
10	5	4.5815	0.418501
11	0.5	3.98529	-3.48529
12	5	4.97895	0.0210505
13	2.5	4.71956	-2.21956
14	5	5.91191	-0.911906
15	5.5	4.78196	0.718043
16	3.5	4.5493	-1.0493
17	4	4.85006	-0.850061
18	6.5	4.67818	1.82182
19	4.5	4.81431	-0.314315
20	5.5	5.28534	0.214661
21	4	4.7516	-0.751604
22	7.5	4.68905	2.81095
23	4	4.38274	-0.382735
24	5.5	3.8151	1.6849
25	2.5	4.62094	-2.12094
26	5.5	5.41415	0.0858503
27	3.5	4.44899	-0.94899
28	4.5	4.24845	0.251546
29	4.5	3.75979	0.740212
30	6	4.74798	1.25202
31	5	3.52343	1.47657
32	6.5	3.59146	2.90854
33	5	4.84829	0.151711
34	6	4.08197	1.91803
35	4.5	3.58968	0.910316
36	5	4.28251	0.717494
37	5	4.78203	0.217965
38	6.5	5.21354	1.28646
39	7	4.38089	2.61911
40	4.5	4.25023	0.249774
41	8.5	6.30936	2.19064
42	3.5	4.14823	-0.648225
43	6	4.25208	1.74792
44	1.5	4.95052	-3.45052
45	3.5	3.95493	-0.454931
46	7.5	4.31479	3.18521
47	5	4.44722	0.552782
48	6.5	4.42411	2.07589
49	6.5	5.31569	1.18431
50	6.5	5.11508	1.38492
51	7	4.15177	2.84823
52	1.5	4.04969	-2.54969
53	4	5.21716	-1.21716
54	4.5	4.31648	0.183519
55	0	3.91726	-3.91726
56	3.5	4.61917	-1.11917
57	4.5	4.88958	-0.389583
58	0	5.01847	-5.01847
59	3	4.98442	-1.98442
60	3.5	4.44899	-0.94899
61	3	5.17949	-2.17949
62	1	4.61917	-3.61917
63	5.5	4.71401	0.785992

Goldfeld-Quandt test for Heteroskedasticity
p-values	Alternative Hypothesis
breakpoint index	greater	2-sided	less
7	0.820077	0.359846	0.179923
8	0.875472	0.249056	0.124528
9	0.857759	0.284481	0.142241
10	0.77754	0.44492	0.22246
11	0.814582	0.370836	0.185418
12	0.745456	0.509089	0.254544
13	0.708495	0.583011	0.291505
14	0.760409	0.479182	0.239591
15	0.683799	0.632401	0.316201
16	0.603751	0.792498	0.396249
17	0.561479	0.877043	0.438521
18	0.611223	0.777554	0.388777
19	0.525369	0.949263	0.474631
20	0.44323	0.88646	0.55677
21	0.375766	0.751532	0.624234
22	0.465053	0.930107	0.534947
23	0.38814	0.776281	0.61186
24	0.430976	0.861951	0.569024
25	0.441795	0.883591	0.558205
26	0.37053	0.74106	0.62947
27	0.31319	0.62638	0.68681
28	0.25403	0.508061	0.74597
29	0.213523	0.427045	0.786477
30	0.177438	0.354875	0.822562
31	0.164106	0.328212	0.835894
32	0.220383	0.440765	0.779617
33	0.16755	0.3351	0.83245
34	0.159676	0.319353	0.840324
35	0.1327	0.2654	0.8673
36	0.099539	0.199078	0.900461
37	0.0697555	0.139511	0.930244
38	0.0542753	0.108551	0.945725
39	0.067502	0.135004	0.932498
40	0.0460065	0.0920129	0.953994
41	0.053241	0.106482	0.946759
42	0.036099	0.0721981	0.963901
43	0.0327762	0.0655525	0.967224
44	0.0697098	0.13942	0.93029
45	0.0464787	0.0929573	0.953521
46	0.0814095	0.162819	0.918591
47	0.0664193	0.132839	0.933581
48	0.118214	0.236428	0.881786
49	0.219877	0.439754	0.780123
50	0.268981	0.537961	0.731019
51	0.387816	0.775631	0.612184
52	0.390958	0.781915	0.609042
53	0.293642	0.587284	0.706358
54	0.200618	0.401236	0.799382
55	0.261579	0.523158	0.738421
56	0.159429	0.318857	0.840571

\begin{tabular}{lllllllll}
\hline
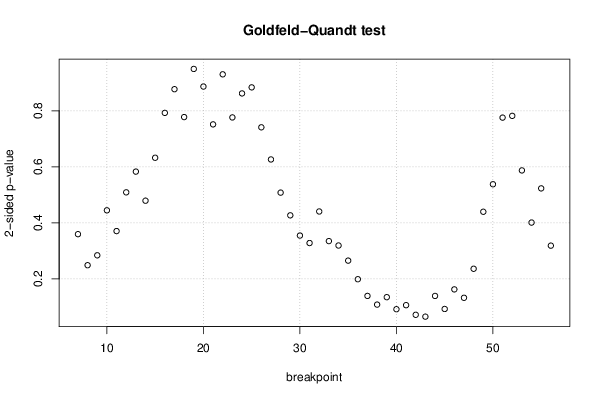
Goldfeld-Quandt test for Heteroskedasticity \tabularnewline
p-values & Alternative Hypothesis \tabularnewline
breakpoint index & greater & 2-sided & less \tabularnewline
7 & 0.820077 & 0.359846 & 0.179923 \tabularnewline
8 & 0.875472 & 0.249056 & 0.124528 \tabularnewline
9 & 0.857759 & 0.284481 & 0.142241 \tabularnewline
10 & 0.77754 & 0.44492 & 0.22246 \tabularnewline
11 & 0.814582 & 0.370836 & 0.185418 \tabularnewline
12 & 0.745456 & 0.509089 & 0.254544 \tabularnewline
13 & 0.708495 & 0.583011 & 0.291505 \tabularnewline
14 & 0.760409 & 0.479182 & 0.239591 \tabularnewline
15 & 0.683799 & 0.632401 & 0.316201 \tabularnewline
16 & 0.603751 & 0.792498 & 0.396249 \tabularnewline
17 & 0.561479 & 0.877043 & 0.438521 \tabularnewline
18 & 0.611223 & 0.777554 & 0.388777 \tabularnewline
19 & 0.525369 & 0.949263 & 0.474631 \tabularnewline
20 & 0.44323 & 0.88646 & 0.55677 \tabularnewline
21 & 0.375766 & 0.751532 & 0.624234 \tabularnewline
22 & 0.465053 & 0.930107 & 0.534947 \tabularnewline
23 & 0.38814 & 0.776281 & 0.61186 \tabularnewline
24 & 0.430976 & 0.861951 & 0.569024 \tabularnewline
25 & 0.441795 & 0.883591 & 0.558205 \tabularnewline
26 & 0.37053 & 0.74106 & 0.62947 \tabularnewline
27 & 0.31319 & 0.62638 & 0.68681 \tabularnewline
28 & 0.25403 & 0.508061 & 0.74597 \tabularnewline
29 & 0.213523 & 0.427045 & 0.786477 \tabularnewline
30 & 0.177438 & 0.354875 & 0.822562 \tabularnewline
31 & 0.164106 & 0.328212 & 0.835894 \tabularnewline
32 & 0.220383 & 0.440765 & 0.779617 \tabularnewline
33 & 0.16755 & 0.3351 & 0.83245 \tabularnewline
34 & 0.159676 & 0.319353 & 0.840324 \tabularnewline
35 & 0.1327 & 0.2654 & 0.8673 \tabularnewline
36 & 0.099539 & 0.199078 & 0.900461 \tabularnewline
37 & 0.0697555 & 0.139511 & 0.930244 \tabularnewline
38 & 0.0542753 & 0.108551 & 0.945725 \tabularnewline
39 & 0.067502 & 0.135004 & 0.932498 \tabularnewline
40 & 0.0460065 & 0.0920129 & 0.953994 \tabularnewline
41 & 0.053241 & 0.106482 & 0.946759 \tabularnewline
42 & 0.036099 & 0.0721981 & 0.963901 \tabularnewline
43 & 0.0327762 & 0.0655525 & 0.967224 \tabularnewline
44 & 0.0697098 & 0.13942 & 0.93029 \tabularnewline
45 & 0.0464787 & 0.0929573 & 0.953521 \tabularnewline
46 & 0.0814095 & 0.162819 & 0.918591 \tabularnewline
47 & 0.0664193 & 0.132839 & 0.933581 \tabularnewline
48 & 0.118214 & 0.236428 & 0.881786 \tabularnewline
49 & 0.219877 & 0.439754 & 0.780123 \tabularnewline
50 & 0.268981 & 0.537961 & 0.731019 \tabularnewline
51 & 0.387816 & 0.775631 & 0.612184 \tabularnewline
52 & 0.390958 & 0.781915 & 0.609042 \tabularnewline
53 & 0.293642 & 0.587284 & 0.706358 \tabularnewline
54 & 0.200618 & 0.401236 & 0.799382 \tabularnewline
55 & 0.261579 & 0.523158 & 0.738421 \tabularnewline
56 & 0.159429 & 0.318857 & 0.840571 \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=265361&T=5

[TABLE]
[ROW][C]Goldfeld-Quandt test for Heteroskedasticity[/C][/ROW]
[ROW][C]p-values[/C][C]Alternative Hypothesis[/C][/ROW]
[ROW][C]breakpoint index[/C][C]greater[/C][C]2-sided[/C][C]less[/C][/ROW]
[ROW][C]7[/C][C]0.820077[/C][C]0.359846[/C][C]0.179923[/C][/ROW]
[ROW][C]8[/C][C]0.875472[/C][C]0.249056[/C][C]0.124528[/C][/ROW]
[ROW][C]9[/C][C]0.857759[/C][C]0.284481[/C][C]0.142241[/C][/ROW]
[ROW][C]10[/C][C]0.77754[/C][C]0.44492[/C][C]0.22246[/C][/ROW]
[ROW][C]11[/C][C]0.814582[/C][C]0.370836[/C][C]0.185418[/C][/ROW]
[ROW][C]12[/C][C]0.745456[/C][C]0.509089[/C][C]0.254544[/C][/ROW]
[ROW][C]13[/C][C]0.708495[/C][C]0.583011[/C][C]0.291505[/C][/ROW]
[ROW][C]14[/C][C]0.760409[/C][C]0.479182[/C][C]0.239591[/C][/ROW]
[ROW][C]15[/C][C]0.683799[/C][C]0.632401[/C][C]0.316201[/C][/ROW]
[ROW][C]16[/C][C]0.603751[/C][C]0.792498[/C][C]0.396249[/C][/ROW]
[ROW][C]17[/C][C]0.561479[/C][C]0.877043[/C][C]0.438521[/C][/ROW]
[ROW][C]18[/C][C]0.611223[/C][C]0.777554[/C][C]0.388777[/C][/ROW]
[ROW][C]19[/C][C]0.525369[/C][C]0.949263[/C][C]0.474631[/C][/ROW]
[ROW][C]20[/C][C]0.44323[/C][C]0.88646[/C][C]0.55677[/C][/ROW]
[ROW][C]21[/C][C]0.375766[/C][C]0.751532[/C][C]0.624234[/C][/ROW]
[ROW][C]22[/C][C]0.465053[/C][C]0.930107[/C][C]0.534947[/C][/ROW]
[ROW][C]23[/C][C]0.38814[/C][C]0.776281[/C][C]0.61186[/C][/ROW]
[ROW][C]24[/C][C]0.430976[/C][C]0.861951[/C][C]0.569024[/C][/ROW]
[ROW][C]25[/C][C]0.441795[/C][C]0.883591[/C][C]0.558205[/C][/ROW]
[ROW][C]26[/C][C]0.37053[/C][C]0.74106[/C][C]0.62947[/C][/ROW]
[ROW][C]27[/C][C]0.31319[/C][C]0.62638[/C][C]0.68681[/C][/ROW]
[ROW][C]28[/C][C]0.25403[/C][C]0.508061[/C][C]0.74597[/C][/ROW]
[ROW][C]29[/C][C]0.213523[/C][C]0.427045[/C][C]0.786477[/C][/ROW]
[ROW][C]30[/C][C]0.177438[/C][C]0.354875[/C][C]0.822562[/C][/ROW]
[ROW][C]31[/C][C]0.164106[/C][C]0.328212[/C][C]0.835894[/C][/ROW]
[ROW][C]32[/C][C]0.220383[/C][C]0.440765[/C][C]0.779617[/C][/ROW]
[ROW][C]33[/C][C]0.16755[/C][C]0.3351[/C][C]0.83245[/C][/ROW]
[ROW][C]34[/C][C]0.159676[/C][C]0.319353[/C][C]0.840324[/C][/ROW]
[ROW][C]35[/C][C]0.1327[/C][C]0.2654[/C][C]0.8673[/C][/ROW]
[ROW][C]36[/C][C]0.099539[/C][C]0.199078[/C][C]0.900461[/C][/ROW]
[ROW][C]37[/C][C]0.0697555[/C][C]0.139511[/C][C]0.930244[/C][/ROW]
[ROW][C]38[/C][C]0.0542753[/C][C]0.108551[/C][C]0.945725[/C][/ROW]
[ROW][C]39[/C][C]0.067502[/C][C]0.135004[/C][C]0.932498[/C][/ROW]
[ROW][C]40[/C][C]0.0460065[/C][C]0.0920129[/C][C]0.953994[/C][/ROW]
[ROW][C]41[/C][C]0.053241[/C][C]0.106482[/C][C]0.946759[/C][/ROW]
[ROW][C]42[/C][C]0.036099[/C][C]0.0721981[/C][C]0.963901[/C][/ROW]
[ROW][C]43[/C][C]0.0327762[/C][C]0.0655525[/C][C]0.967224[/C][/ROW]
[ROW][C]44[/C][C]0.0697098[/C][C]0.13942[/C][C]0.93029[/C][/ROW]
[ROW][C]45[/C][C]0.0464787[/C][C]0.0929573[/C][C]0.953521[/C][/ROW]
[ROW][C]46[/C][C]0.0814095[/C][C]0.162819[/C][C]0.918591[/C][/ROW]
[ROW][C]47[/C][C]0.0664193[/C][C]0.132839[/C][C]0.933581[/C][/ROW]
[ROW][C]48[/C][C]0.118214[/C][C]0.236428[/C][C]0.881786[/C][/ROW]
[ROW][C]49[/C][C]0.219877[/C][C]0.439754[/C][C]0.780123[/C][/ROW]
[ROW][C]50[/C][C]0.268981[/C][C]0.537961[/C][C]0.731019[/C][/ROW]
[ROW][C]51[/C][C]0.387816[/C][C]0.775631[/C][C]0.612184[/C][/ROW]
[ROW][C]52[/C][C]0.390958[/C][C]0.781915[/C][C]0.609042[/C][/ROW]
[ROW][C]53[/C][C]0.293642[/C][C]0.587284[/C][C]0.706358[/C][/ROW]
[ROW][C]54[/C][C]0.200618[/C][C]0.401236[/C][C]0.799382[/C][/ROW]
[ROW][C]55[/C][C]0.261579[/C][C]0.523158[/C][C]0.738421[/C][/ROW]
[ROW][C]56[/C][C]0.159429[/C][C]0.318857[/C][C]0.840571[/C][/ROW]
[/TABLE]
Source: https://freestatistics.org/blog/index.php?pk=265361&T=5

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=265361&T=5

As an alternative you can also use a QR Code:

The GUIDs for individual cells are displayed in the table below:

Goldfeld-Quandt test for Heteroskedasticity
p-values	Alternative Hypothesis
breakpoint index	greater	2-sided	less
7	0.820077	0.359846	0.179923
8	0.875472	0.249056	0.124528
9	0.857759	0.284481	0.142241
10	0.77754	0.44492	0.22246
11	0.814582	0.370836	0.185418
12	0.745456	0.509089	0.254544
13	0.708495	0.583011	0.291505
14	0.760409	0.479182	0.239591
15	0.683799	0.632401	0.316201
16	0.603751	0.792498	0.396249
17	0.561479	0.877043	0.438521
18	0.611223	0.777554	0.388777
19	0.525369	0.949263	0.474631
20	0.44323	0.88646	0.55677
21	0.375766	0.751532	0.624234
22	0.465053	0.930107	0.534947
23	0.38814	0.776281	0.61186
24	0.430976	0.861951	0.569024
25	0.441795	0.883591	0.558205
26	0.37053	0.74106	0.62947
27	0.31319	0.62638	0.68681
28	0.25403	0.508061	0.74597
29	0.213523	0.427045	0.786477
30	0.177438	0.354875	0.822562
31	0.164106	0.328212	0.835894
32	0.220383	0.440765	0.779617
33	0.16755	0.3351	0.83245
34	0.159676	0.319353	0.840324
35	0.1327	0.2654	0.8673
36	0.099539	0.199078	0.900461
37	0.0697555	0.139511	0.930244
38	0.0542753	0.108551	0.945725
39	0.067502	0.135004	0.932498
40	0.0460065	0.0920129	0.953994
41	0.053241	0.106482	0.946759
42	0.036099	0.0721981	0.963901
43	0.0327762	0.0655525	0.967224
44	0.0697098	0.13942	0.93029
45	0.0464787	0.0929573	0.953521
46	0.0814095	0.162819	0.918591
47	0.0664193	0.132839	0.933581
48	0.118214	0.236428	0.881786
49	0.219877	0.439754	0.780123
50	0.268981	0.537961	0.731019
51	0.387816	0.775631	0.612184
52	0.390958	0.781915	0.609042
53	0.293642	0.587284	0.706358
54	0.200618	0.401236	0.799382
55	0.261579	0.523158	0.738421
56	0.159429	0.318857	0.840571

Meta Analysis of Goldfeld-Quandt test for Heteroskedasticity
Description	# significant tests	% significant tests	OK/NOK
1% type I error level	0	0	OK
5% type I error level	0	0	OK
10% type I error level	4	0.08	OK

\begin{tabular}{lllllllll}
\hline
Meta Analysis of Goldfeld-Quandt test for Heteroskedasticity \tabularnewline
Description & # significant tests & % significant tests & OK/NOK \tabularnewline
1% type I error level & 0 & 0 & OK \tabularnewline
5% type I error level & 0 & 0 & OK \tabularnewline
10% type I error level & 4 & 0.08 & OK \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=265361&T=6

[TABLE]
[ROW][C]Meta Analysis of Goldfeld-Quandt test for Heteroskedasticity[/C][/ROW]
[ROW][C]Description[/C][C]# significant tests[/C][C]% significant tests[/C][C]OK/NOK[/C][/ROW]
[ROW][C]1% type I error level[/C][C]0[/C][C]0[/C][C]OK[/C][/ROW]
[ROW][C]5% type I error level[/C][C]0[/C][C]0[/C][C]OK[/C][/ROW]
[ROW][C]10% type I error level[/C][C]4[/C][C]0.08[/C][C]OK[/C][/ROW]
[/TABLE]
Source: https://freestatistics.org/blog/index.php?pk=265361&T=6

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=265361&T=6

As an alternative you can also use a QR Code:

The GUIDs for individual cells are displayed in the table below:

Meta Analysis of Goldfeld-Quandt test for Heteroskedasticity
Description	# significant tests	% significant tests	OK/NOK
1% type I error level	0	0	OK
5% type I error level	0	0	OK
10% type I error level	4	0.08	OK

Figure 1

PNG link

Postscript link

PDF link

Figure 2

PNG link

Postscript link

PDF link

Figure 3

PNG link

Postscript link

PDF link

Figure 4

PNG link

Postscript link

PDF link

Figure 5

PNG link

Postscript link

PDF link

Figure 6

PNG link

Postscript link

PDF link

Figure 7

PNG link

Postscript link

PDF link

Figure 8

PNG link

Postscript link

PDF link

Figure 9

PNG link

Postscript link

PDF link

Figure 10

PNG link

Postscript link

PDF link

Parameters (Session):

par1 = 1 ; par2 = Do not include Seasonal Dummies ; par3 = No Linear Trend ;

Parameters (R input):

par1 = 1 ; par2 = Do not include Seasonal Dummies ; par3 = No Linear Trend ;

R code (references can be found in the software module):

library(lattice)
library(lmtest)
n25 <- 25 #minimum number of obs. for Goldfeld-Quandt test
par1 <- as.numeric(par1)
x <- t(y)
k <- length(x[1,])
n <- length(x[,1])
x1 <- cbind(x[,par1], x[,1:k!=par1])
mycolnames <- c(colnames(x)[par1], colnames(x)[1:k!=par1])
colnames(x1) <- mycolnames #colnames(x)[par1]
x <- x1
if (par3 == 'First Differences'){
x2 <- array(0, dim=c(n-1,k), dimnames=list(1:(n-1), paste('(1-B)',colnames(x),sep='')))
for (i in 1:n-1) {
for (j in 1:k) {
x2[i,j] <- x[i+1,j] - x[i,j]
}
}
x <- x2
}
if (par2 == 'Include Monthly Dummies'){
x2 <- array(0, dim=c(n,11), dimnames=list(1:n, paste('M', seq(1:11), sep ='')))
for (i in 1:11){
x2[seq(i,n,12),i] <- 1
}
x <- cbind(x, x2)
}
if (par2 == 'Include Quarterly Dummies'){
x2 <- array(0, dim=c(n,3), dimnames=list(1:n, paste('Q', seq(1:3), sep ='')))
for (i in 1:3){
x2[seq(i,n,4),i] <- 1
}
x <- cbind(x, x2)
}
k <- length(x[1,])
if (par3 == 'Linear Trend'){
x <- cbind(x, c(1:n))
colnames(x)[k+1] <- 't'
}
x
k <- length(x[1,])
df <- as.data.frame(x)
(mylm <- lm(df))
(mysum <- summary(mylm))
if (n > n25) {
kp3 <- k + 3
nmkm3 <- n - k - 3
gqarr <- array(NA, dim=c(nmkm3-kp3+1,3))
numgqtests <- 0
numsignificant1 <- 0
numsignificant5 <- 0
numsignificant10 <- 0
for (mypoint in kp3:nmkm3) {
j <- 0
numgqtests <- numgqtests + 1
for (myalt in c('greater', 'two.sided', 'less')) {
j <- j + 1
gqarr[mypoint-kp3+1,j] <- gqtest(mylm, point=mypoint, alternative=myalt)$p.value
}
if (gqarr[mypoint-kp3+1,2] < 0.01) numsignificant1 <- numsignificant1 + 1
if (gqarr[mypoint-kp3+1,2] < 0.05) numsignificant5 <- numsignificant5 + 1
if (gqarr[mypoint-kp3+1,2] < 0.10) numsignificant10 <- numsignificant10 + 1
}
gqarr
}
bitmap(file='test0.png')
plot(x[,1], type='l', main='Actuals and Interpolation', ylab='value of Actuals and Interpolation (dots)', xlab='time or index')
points(x[,1]-mysum$resid)
grid()
dev.off()
bitmap(file='test1.png')
plot(mysum$resid, type='b', pch=19, main='Residuals', ylab='value of Residuals', xlab='time or index')
grid()
dev.off()
bitmap(file='test2.png')
hist(mysum$resid, main='Residual Histogram', xlab='values of Residuals')
grid()
dev.off()
bitmap(file='test3.png')
densityplot(~mysum$resid,col='black',main='Residual Density Plot', xlab='values of Residuals')
dev.off()
bitmap(file='test4.png')
qqnorm(mysum$resid, main='Residual Normal Q-Q Plot')
qqline(mysum$resid)
grid()
dev.off()
(myerror <- as.ts(mysum$resid))
bitmap(file='test5.png')
dum <- cbind(lag(myerror,k=1),myerror)
dum
dum1 <- dum[2:length(myerror),]
dum1
z <- as.data.frame(dum1)
z
plot(z,main=paste('Residual Lag plot, lowess, and regression line'), ylab='values of Residuals', xlab='lagged values of Residuals')
lines(lowess(z))
abline(lm(z))
grid()
dev.off()
bitmap(file='test6.png')
acf(mysum$resid, lag.max=length(mysum$resid)/2, main='Residual Autocorrelation Function')
grid()
dev.off()
bitmap(file='test7.png')
pacf(mysum$resid, lag.max=length(mysum$resid)/2, main='Residual Partial Autocorrelation Function')
grid()
dev.off()
bitmap(file='test8.png')
opar <- par(mfrow = c(2,2), oma = c(0, 0, 1.1, 0))
plot(mylm, las = 1, sub='Residual Diagnostics')
par(opar)
dev.off()
if (n > n25) {
bitmap(file='test9.png')
plot(kp3:nmkm3,gqarr[,2], main='Goldfeld-Quandt test',ylab='2-sided p-value',xlab='breakpoint')
grid()
dev.off()
}
load(file='createtable')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a, 'Multiple Linear Regression - Estimated Regression Equation', 1, TRUE)
a<-table.row.end(a)
myeq <- colnames(x)[1]
myeq <- paste(myeq, '[t] = ', sep='')
for (i in 1:k){
if (mysum$coefficients[i,1] > 0) myeq <- paste(myeq, '+', '')
myeq <- paste(myeq, signif(mysum$coefficients[i,1],6), sep=' ')
if (rownames(mysum$coefficients)[i] != '(Intercept)') {
myeq <- paste(myeq, rownames(mysum$coefficients)[i], sep='')
if (rownames(mysum$coefficients)[i] != 't') myeq <- paste(myeq, '[t]', sep='')
}
}
myeq <- paste(myeq, ' + e[t]')
a<-table.row.start(a)
a<-table.element(a, myeq)
a<-table.row.end(a)
a<-table.end(a)
table.save(a,file='mytable1.tab')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a,hyperlink('ols1.htm','Multiple Linear Regression - Ordinary Least Squares',''), 6, TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'Variable',header=TRUE)
a<-table.element(a,'Parameter',header=TRUE)
a<-table.element(a,'S.D.',header=TRUE)
a<-table.element(a,'T-STAT
H0: parameter = 0',header=TRUE)
a<-table.element(a,'2-tail p-value',header=TRUE)
a<-table.element(a,'1-tail p-value',header=TRUE)
a<-table.row.end(a)
for (i in 1:k){
a<-table.row.start(a)
a<-table.element(a,rownames(mysum$coefficients)[i],header=TRUE)
a<-table.element(a,signif(mysum$coefficients[i,1],6))
a<-table.element(a, signif(mysum$coefficients[i,2],6))
a<-table.element(a, signif(mysum$coefficients[i,3],4))
a<-table.element(a, signif(mysum$coefficients[i,4],6))
a<-table.element(a, signif(mysum$coefficients[i,4]/2,6))
a<-table.row.end(a)
}
a<-table.end(a)
table.save(a,file='mytable2.tab')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a, 'Multiple Linear Regression - Regression Statistics', 2, TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'Multiple R',1,TRUE)
a<-table.element(a, signif(sqrt(mysum$r.squared),6))
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'R-squared',1,TRUE)
a<-table.element(a, signif(mysum$r.squared,6))
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'Adjusted R-squared',1,TRUE)
a<-table.element(a, signif(mysum$adj.r.squared,6))
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'F-TEST (value)',1,TRUE)
a<-table.element(a, signif(mysum$fstatistic[1],6))
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'F-TEST (DF numerator)',1,TRUE)
a<-table.element(a, signif(mysum$fstatistic[2],6))
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'F-TEST (DF denominator)',1,TRUE)
a<-table.element(a, signif(mysum$fstatistic[3],6))
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'p-value',1,TRUE)
a<-table.element(a, signif(1-pf(mysum$fstatistic[1],mysum$fstatistic[2],mysum$fstatistic[3]),6))
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'Multiple Linear Regression - Residual Statistics', 2, TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'Residual Standard Deviation',1,TRUE)
a<-table.element(a, signif(mysum$sigma,6))
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'Sum Squared Residuals',1,TRUE)
a<-table.element(a, signif(sum(myerror*myerror),6))
a<-table.row.end(a)
a<-table.end(a)
table.save(a,file='mytable3.tab')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a, 'Multiple Linear Regression - Actuals, Interpolation, and Residuals', 4, TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'Time or Index', 1, TRUE)
a<-table.element(a, 'Actuals', 1, TRUE)
a<-table.element(a, 'Interpolation
Forecast', 1, TRUE)
a<-table.element(a, 'Residuals
Prediction Error', 1, TRUE)
a<-table.row.end(a)
for (i in 1:n) {
a<-table.row.start(a)
a<-table.element(a,i, 1, TRUE)
a<-table.element(a,signif(x[i],6))
a<-table.element(a,signif(x[i]-mysum$resid[i],6))
a<-table.element(a,signif(mysum$resid[i],6))
a<-table.row.end(a)
}
a<-table.end(a)
table.save(a,file='mytable4.tab')
if (n > n25) {
a<-table.start()
a<-table.row.start(a)
a<-table.element(a,'Goldfeld-Quandt test for Heteroskedasticity',4,TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'p-values',header=TRUE)
a<-table.element(a,'Alternative Hypothesis',3,header=TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'breakpoint index',header=TRUE)
a<-table.element(a,'greater',header=TRUE)
a<-table.element(a,'2-sided',header=TRUE)
a<-table.element(a,'less',header=TRUE)
a<-table.row.end(a)
for (mypoint in kp3:nmkm3) {
a<-table.row.start(a)
a<-table.element(a,mypoint,header=TRUE)
a<-table.element(a,signif(gqarr[mypoint-kp3+1,1],6))
a<-table.element(a,signif(gqarr[mypoint-kp3+1,2],6))
a<-table.element(a,signif(gqarr[mypoint-kp3+1,3],6))
a<-table.row.end(a)
}
a<-table.end(a)
table.save(a,file='mytable5.tab')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a,'Meta Analysis of Goldfeld-Quandt test for Heteroskedasticity',4,TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'Description',header=TRUE)
a<-table.element(a,'# significant tests',header=TRUE)
a<-table.element(a,'% significant tests',header=TRUE)
a<-table.element(a,'OK/NOK',header=TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'1% type I error level',header=TRUE)
a<-table.element(a,signif(numsignificant1,6))
a<-table.element(a,signif(numsignificant1/numgqtests,6))
if (numsignificant1/numgqtests < 0.01) dum <- 'OK' else dum <- 'NOK'
a<-table.element(a,dum)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'5% type I error level',header=TRUE)
a<-table.element(a,signif(numsignificant5,6))
a<-table.element(a,signif(numsignificant5/numgqtests,6))
if (numsignificant5/numgqtests < 0.05) dum <- 'OK' else dum <- 'NOK'
a<-table.element(a,dum)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'10% type I error level',header=TRUE)
a<-table.element(a,signif(numsignificant10,6))
a<-table.element(a,signif(numsignificant10/numgqtests,6))
if (numsignificant10/numgqtests < 0.1) dum <- 'OK' else dum <- 'NOK'
a<-table.element(a,dum)
a<-table.row.end(a)
a<-table.end(a)
table.save(a,file='mytable6.tab')
}

Free Statistics

Description of Statistical Computation

Tree of Dependent Computations

Dataset

Tables (Output of Computation)

Figures (Output of Computation)

Input Parameters & R Code