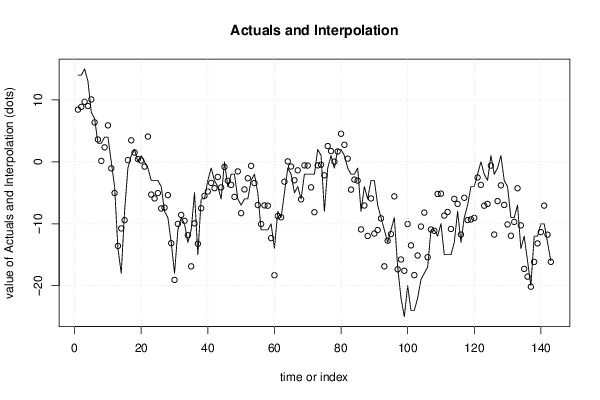
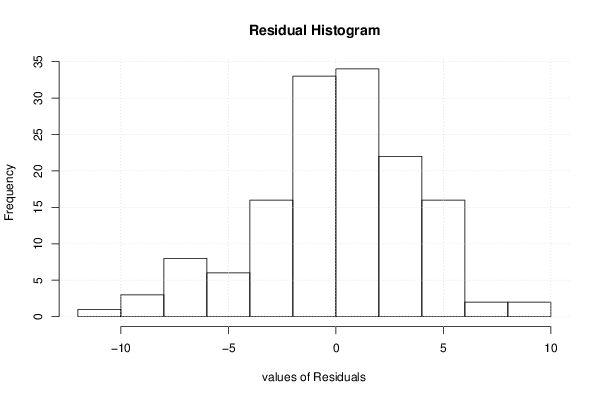
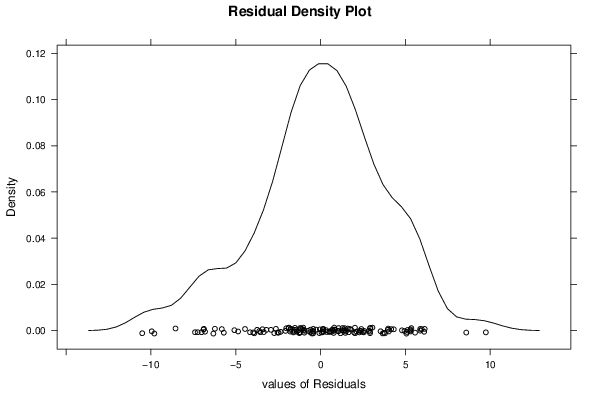
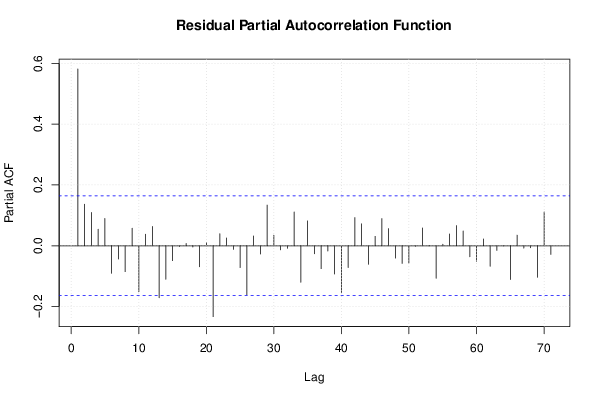
14 501 11 20 91,81 77585 1303,2 13
14 485 11 19 91,98 77585 -58,7 15
15 464 11 18 91,72 77585 -378,9 3
13 460 11 13 90,27 78302 175,6 2
8 467 11 17 91,89 78302 233,7 -2
7 460 9 17 92,07 78302 706,8 1
3 448 8 13 92,92 78224 -23,6 1
3 443 6 14 93,34 78224 420,9 -1
4 436 7 13 93,6 78224 722,1 -6
4 431 8 17 92,41 78178 1401,3 -13
0 484 6 17 93,6 78178 -94,9 -25
-4 510 5 15 93,77 78178 1043,6 -26
-14 513 2 9 93,6 77988 1300,1 -9
-18 503 3 10 93,6 77988 721,1 1
-8 471 3 9 93,51 77988 -45,6 3
-1 471 7 14 92,66 77876 787,5 6
1 476 8 18 94,2 77876 694,3 2
2 475 7 18 94,37 77876 1054,7 5
0 470 7 12 94,45 78432 821,9 5
1 461 6 16 94,62 78432 1100,7 0
0 455 6 12 94,37 78432 862,4 -5
-1 456 7 19 93,43 79025 1656,1 -4
-3 517 5 13 94,79 79025 -174 -2
-3 525 5 12 94,88 79025 1337,6 -1
-3 523 5 13 94,79 79407 1394,9 -8
-4 519 4 11 94,62 79407 915,7 -16
-8 509 4 10 94,71 79407 -481,1 -19
-9 512 4 16 93,77 79644 167,9 -28
-13 519 1 12 95,73 79644 208,2 -11
-18 517 -1 6 95,99 79644 382,2 -4
-11 510 3 8 95,82 79381 1004 -9
-9 509 4 6 95,47 79381 864,7 -12
-10 501 3 8 95,82 79381 1052,9 -10
-13 507 2 8 94,71 79536 1417,6 -2
-11 569 1 9 96,33 79536 -197,7 -13
-5 580 4 13 96,5 79536 1262,1 0
-15 578 3 8 96,16 79813 1147,2 0
-6 565 5 11 96,33 79813 700,2 4
-6 547 6 8 96,33 79813 45,3 7
-3 555 6 10 95,05 80332 458,5 5
-1 562 6 15 96,84 80332 610,2 2
-3 561 6 12 96,92 80332 786,4 -2
-4 555 6 13 97,44 81434 787,2 6
-6 544 5 12 97,78 81434 1040 -3
0 537 6 15 97,69 81434 324,1 1
-4 543 5 13 96,67 82167 1343 0
-2 594 6 13 98,29 82167 -501,2 -7
-2 611 5 16 98,2 82167 800,4 -6
-6 613 7 14 98,71 82816 916,7 -4
-7 611 4 12 98,54 82816 695,8 -4
-6 594 5 15 98,2 82816 28 -2
-6 595 6 14 96,92 83000 495,6 2
-3 591 6 19 99,06 83000 366,2 -5
-2 589 5 16 99,65 83000 633 -15
-5 584 3 16 99,82 83251 848,3 -16
-11 573 2 11 99,99 83251 472,2 -18
-11 567 3 13 100,33 83251 357,8 -13
-11 569 3 12 99,31 83591 824,3 -23
-10 621 2 11 101,1 83591 -880,1 -10
-14 629 0 6 101,1 83591 1066,8 -10
-8 628 4 9 100,93 83910 1052,8 -6
-9 612 4 6 100,85 83910 -32,1 -3
-5 595 5 15 100,93 83910 -1331,4 -4
-1 597 6 17 99,6 84599 -767,1 -7
-2 593 6 13 101,88 84599 -236,7 -7
-5 590 5 12 101,81 84599 -184,9 -7
-4 580 5 13 102,38 85275 -143,4 -3
-6 574 3 10 102,74 85275 493,9 0
-2 573 5 14 102,82 85275 549,7 -5
-2 573 5 13 101,72 85608 982,7 -3
-2 620 5 10 103,47 85608 -856,3 3
-2 626 3 11 102,98 85608 967 2
2 620 6 12 102,68 86303 659,4 -7
1 588 6 7 102,9 86303 577,2 -1
-8 566 4 11 103,03 86303 -213,1 0
-1 557 6 9 101,29 87115 17,7 -3
1 561 5 13 103,69 87115 390,1 4
-1 549 4 12 103,68 87115 509,3 2
2 532 5 5 104,2 87931 410 3
2 526 5 13 104,08 87931 212,5 0
1 511 4 11 104,16 87931 818 -10
-1 499 3 8 103,05 88164 422,7 -10
-2 555 2 8 104,66 88164 -158 -9
-2 565 3 8 104,46 88164 427,2 -22
-1 542 2 8 104,95 88792 243,4 -16
-8 527 -1 0 105,85 88792 -419,3 -18
-4 510 0 3 106,23 88792 -1459,8 -14
-6 514 -2 0 104,86 89263 -1389,8 -12
-3 517 1 -1 107,44 89263 -2,1 -17
-3 508 -2 -1 108,23 89263 -938,6 -23
-7 493 -2 -4 108,45 89881 -839,9 -28
-9 490 -2 1 109,39 89881 -297,6 -31
-11 469 -6 -1 110,15 89881 -376,3 -21
-13 478 -4 0 109,13 90120 -79,4 -19
-11 528 -2 -1 110,28 90120 -2091,3 -22
-9 534 0 6 110,17 90120 -1023 -22
-17 518 -5 0 109,99 89703 -765,6 -25
-22 506 -4 -3 109,26 89703 -1592,3 -16
-25 502 -5 -3 109,11 89703 -1588,8 -22
-20 516 -1 4 107,06 87818 -1318 -21
-24 528 -2 1 109,53 87818 -402,4 -10
-24 533 -4 0 108,92 87818 -814,5 -7
-22 536 -1 -4 109,24 86273 -98,4 -5
-19 537 1 -2 109,12 86273 -305,9 -4
-18 524 1 3 109 86273 -18,4 7
-17 536 -2 2 107,23 86316 610,3 6
-11 587 1 5 109,49 86316 -917,3 3
-11 597 1 6 109,04 86316 88,4 10
-12 581 3 6 109,02 87234 -740,2 0
-10 564 3 3 109,23 87234 29,3 -2
-15 558 1 4 109,46 87234 -893,2 -1
-15 575 1 7 107,9 87885 -1030,2 2
-15 580 0 5 110,42 87885 -403,4 8
-13 575 2 6 110,98 87885 -46,9 -6
-8 563 2 1 111,48 88003 -321,2 -4
-13 552 -1 3 111,88 88003 -239,9 4
-9 537 1 6 111,89 88003 640,9 7
-7 545 0 0 109,85 88910 511,6 3
-4 601 1 3 112,1 88910 -665,1 3
-4 604 1 4 112,24 88910 657,7 8
-2 586 3 7 112,39 89397 -207,7 3
0 564 2 6 112,52 89397 -885,2 -3
-2 549 0 6 113,16 89397 -1595,8 4
-3 551 0 6 111,84 89813 -1374,9 -5
1 556 3 6 114,33 89813 -316,6 -1
-2 548 -2 2 114,82 89813 -283,4 5
-1 540 0 2 115,2 90539 -175,8 0
1 531 1 2 115,4 90539 -694,2 -6
-3 521 -1 3 115,74 90539 -249,9 -13
-4 519 -2 -1 114,19 90688 268,2 -15
-9 572 -1 -4 115,94 90688 -2105,1 -8
-9 581 -1 4 116,03 90688 -762,8 -20
-7 563 1 5 116,24 90691 -117,1 -10
-14 548 -2 3 116,66 90691 -1094,4 -22
-12 539 -5 -1 116,79 90691 -2095,2 -25
-16 541 -5 -4 115,48 90645 -1587,6 -10
-20 562 -6 0 118,16 90645 -528 -8
-12 559 -4 -1 118,38 90645 -324,2 -9
-12 546 -3 -1 118,51 90861 -276,1 -5
-10 536 -3 3 118,42 90861 -139,1 -7
-10 528 -1 2 118,24 90861 268 -11
-13 530 -2 -4 116,47 90401 570,5 -11
-16 582 -3 -3 118,96 90401 -316,5 -16
|