Repository of Reproducible Computations

Free Statistics

of Irreproducible Research!

Author's title

Author

*Unverified author*

R Software Module

rwasp_exponentialsmoothing.wasp

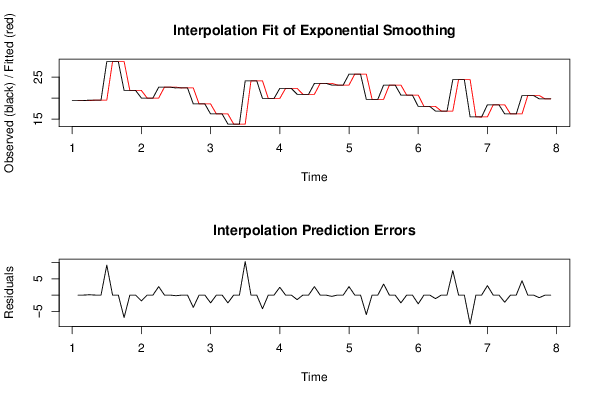
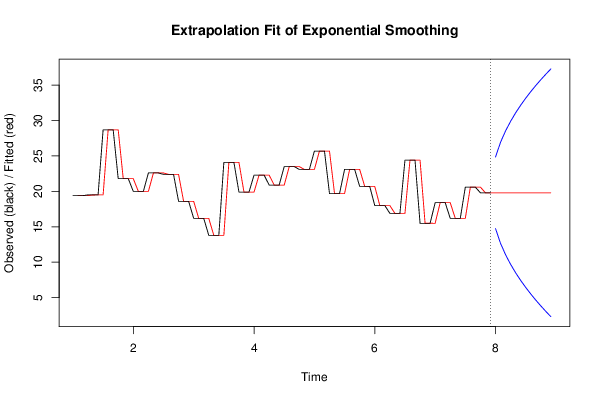
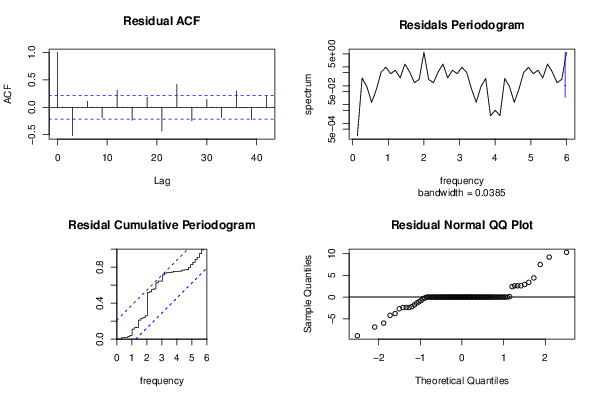
Title produced by software

Exponential Smoothing

Date of computation

Thu, 12 Dec 2013 02:35:50 -0500

Cite this page as follows

Statistical Computations at FreeStatistics.org, Office for Research Development and Education, URL https://freestatistics.org/blog/index.php?v=date/2013/Dec/12/t1386833978pejo9lrb4cwikey.htm/, Retrieved Tue, 23 Apr 2024 06:22:51 +0000

Statistical Computations at FreeStatistics.org, Office for Research Development and Education, URL https://freestatistics.org/blog/index.php?pk=232209, Retrieved Tue, 23 Apr 2024 06:22:51 +0000

QR Codes:

Paste this QR Code to cite your computation.

Original text written by user:

IsPrivate?

No (this computation is public)

User-defined keywords

Estimated Impact

104

Family? (F = Feedback message, R = changed R code, M = changed R Module, P = changed Parameters, D = changed Data)

-       [Exponential Smoothing] [] [2013-12-12 07:35:50] [20efb5145ec2a2ddd8dcd418764211fa] [Current]

Feedback Forum

Post a new message

Dataseries X:

Download CSV

Histogram

Boxplots

Summary of computational transaction
Raw Input	view raw input (R code)
Raw Output	view raw output of R engine
Computing time	5 seconds
R Server	'Gwilym Jenkins' @ jenkins.wessa.net

\begin{tabular}{lllllllll}
\hline
Summary of computational transaction \tabularnewline
Raw Input & view raw input (R code)  \tabularnewline
Raw Output & view raw output of R engine  \tabularnewline
Computing time & 5 seconds \tabularnewline
R Server & 'Gwilym Jenkins' @ jenkins.wessa.net \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=232209&T=0

[TABLE]
[ROW][C]Summary of computational transaction[/C][/ROW]
[ROW][C]Raw Input[/C][C]view raw input (R code) [/C][/ROW]
[ROW][C]Raw Output[/C][C]view raw output of R engine [/C][/ROW]
[ROW][C]Computing time[/C][C]5 seconds[/C][/ROW]
[ROW][C]R Server[/C][C]'Gwilym Jenkins' @ jenkins.wessa.net[/C][/ROW]
[/TABLE]
Source: https://freestatistics.org/blog/index.php?pk=232209&T=0

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=232209&T=0

As an alternative you can also use a QR Code:

The GUIDs for individual cells are displayed in the table below:

Summary of computational transaction
Raw Input	view raw input (R code)
Raw Output	view raw output of R engine
Computing time	5 seconds
R Server	'Gwilym Jenkins' @ jenkins.wessa.net

Estimated Parameters of Exponential Smoothing
Parameter	Value
alpha	0.999933893038648
beta	FALSE
gamma	FALSE

\begin{tabular}{lllllllll}
\hline
Estimated Parameters of Exponential Smoothing \tabularnewline
Parameter & Value \tabularnewline
alpha & 0.999933893038648 \tabularnewline
beta & FALSE \tabularnewline
gamma & FALSE \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=232209&T=1

[TABLE]
[ROW][C]Estimated Parameters of Exponential Smoothing[/C][/ROW]
[ROW][C]Parameter[/C][C]Value[/C][/ROW]
[ROW][C]alpha[/C][C]0.999933893038648[/C][/ROW]
[ROW][C]beta[/C][C]FALSE[/C][/ROW]
[ROW][C]gamma[/C][C]FALSE[/C][/ROW]
[/TABLE]
Source: https://freestatistics.org/blog/index.php?pk=232209&T=1

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=232209&T=1

As an alternative you can also use a QR Code:

The GUIDs for individual cells are displayed in the table below:

Estimated Parameters of Exponential Smoothing
Parameter	Value
alpha	0.999933893038648
beta	FALSE
gamma	FALSE

Interpolation Forecasts of Exponential Smoothing
t	Observed	Fitted	Residuals
2	19.4	19.4	0
3	19.4	19.4	0
4	19.5	19.4	0.100000000000001
5	19.5	19.4999933893039	6.61069613627774e-06
6	19.5	19.499999999563	4.37012204201892e-10
7	28.7	19.5	9.20000000000003
8	28.7	28.6993918159556	0.000608184044438076
9	28.7	28.6999999597948	4.02051973935613e-08
10	21.8	28.6999999999973	-6.89999999999734
11	21.8	21.8004561380333	-0.000456138033328557
12	21.8	21.8000000301539	-3.01538989333494e-08
13	20	21.800000000002	-1.80000000000199
14	20	20.0001189925304	-0.000118992530435236
15	20	20.0000000078662	-7.86623388648877e-09
16	22.6	20.0000000000005	2.59999999999948
17	22.6	22.5998281219005	0.000171878099514799
18	22.6	22.5999999886377	1.13623386255313e-08
19	22.4	22.5999999999993	-0.199999999999253
20	22.4	22.4000132213923	-1.32213922690028e-05
21	22.4	22.400000000874	-8.74024408403784e-10
22	18.6	22.4000000000001	-3.80000000000005
23	18.6	18.6002512064531	-0.000251206453135921
24	18.6	18.6000000166065	-1.6606495734095e-08
25	16.2	18.6000000000011	-2.4000000000011
26	16.2	16.2001586567072	-0.000158656707245797
27	16.2	16.2000000104883	-1.04883142171275e-08
28	13.8	16.2000000000007	-2.40000000000069
29	13.8	13.8001586567072	-0.00015865670724402
30	13.8	13.8000000104883	-1.04883124407706e-08
31	24.1	13.8000000000007	10.2999999999993
32	24.1	24.0993190982981	0.00068090170192292
33	24.1	24.0999999549877	4.50123422979232e-08
34	19.9	24.099999999997	-4.19999999999703
35	19.9	19.9002776492377	-0.00027764923767748
36	19.9	19.9000000183545	-1.83545481036163e-08
37	22.3	19.9000000000012	2.39999999999879
38	22.3	22.2998413432928	0.000158656707245797
39	22.3	22.2999999895117	1.04883142171275e-08
40	20.9	22.2999999999993	-1.39999999999931
41	20.9	20.9000925497459	-9.25497458936775e-05
42	20.9	20.9000000061182	-6.11818151696752e-09
43	23.5	20.9000000000004	2.5999999999996
44	23.5	23.4998281219005	0.000171878099514799
45	23.5	23.4999999886377	1.13623386255313e-08
46	23.1	23.4999999999993	-0.399999999999249
47	23.1	23.1000264427845	-2.64427845415582e-05
48	23.1	23.1000000017481	-1.74805236952125e-09
49	25.7	23.1000000000001	2.59999999999988
50	25.7	25.6998281219005	0.000171878099514799
51	25.7	25.6999999886377	1.13623386255313e-08
52	19.7	25.6999999999992	-5.99999999999925
53	19.7	19.7003966417681	-0.000396641768112715
54	19.7	19.7000000262208	-2.6220781990105e-08
55	23.1	19.7000000000017	3.39999999999827
56	23.1	23.0997752363314	0.000224763668597916
57	23.1	23.0999999851416	1.48584433645738e-08
58	20.7	23.099999999999	-2.39999999999902
59	20.7	20.7001586567072	-0.000158656707245797
60	20.7	20.7000000104883	-1.04883142171275e-08
61	18	20.7000000000007	-2.70000000000069
62	18	18.0001784887957	-0.000178488795651077
63	18	18.0000000117994	-1.17993508297332e-08
64	16.9	18.0000000000008	-1.10000000000078
65	16.9	16.9000727176575	-7.2717657488397e-05
66	16.9	16.9000000048071	-4.80714490436185e-09
67	24.4	16.9000000000003	7.49999999999968
68	24.4	24.3995041977899	0.000495802210139118
69	24.4	24.399999967224	3.27759792639881e-08
70	15.5	24.3999999999978	-8.89999999999783
71	15.5	15.500588351956	-0.000588351956031019
72	15.5	15.5000000388942	-3.88941607809556e-08
73	18.4	15.5000000000026	2.89999999999743
74	18.4	18.3998082898121	0.00019171018792008
75	18.4	18.3999999873266	1.26733787908506e-08
76	16.2	18.3999999999992	-2.19999999999916
77	16.2	16.200145435315	-0.000145435314973241
78	16.2	16.2000000096143	-9.61428625601002e-09
79	20.6	16.2000000000006	4.39999999999937
80	20.6	20.5997091293701	0.000290870629950035
81	20.6	20.5999999807714	1.922857251202e-08
82	19.8	20.5999999999987	-0.799999999998729
83	19.8	19.8000528855691	-5.28855690831165e-05
84	19.8	19.8000000034961	-3.49610473904249e-09

\begin{tabular}{lllllllll}
\hline
Interpolation Forecasts of Exponential Smoothing \tabularnewline
t & Observed & Fitted & Residuals \tabularnewline
2 & 19.4 & 19.4 & 0 \tabularnewline
3 & 19.4 & 19.4 & 0 \tabularnewline
4 & 19.5 & 19.4 & 0.100000000000001 \tabularnewline
5 & 19.5 & 19.4999933893039 & 6.61069613627774e-06 \tabularnewline
6 & 19.5 & 19.499999999563 & 4.37012204201892e-10 \tabularnewline
7 & 28.7 & 19.5 & 9.20000000000003 \tabularnewline
8 & 28.7 & 28.6993918159556 & 0.000608184044438076 \tabularnewline
9 & 28.7 & 28.6999999597948 & 4.02051973935613e-08 \tabularnewline
10 & 21.8 & 28.6999999999973 & -6.89999999999734 \tabularnewline
11 & 21.8 & 21.8004561380333 & -0.000456138033328557 \tabularnewline
12 & 21.8 & 21.8000000301539 & -3.01538989333494e-08 \tabularnewline
13 & 20 & 21.800000000002 & -1.80000000000199 \tabularnewline
14 & 20 & 20.0001189925304 & -0.000118992530435236 \tabularnewline
15 & 20 & 20.0000000078662 & -7.86623388648877e-09 \tabularnewline
16 & 22.6 & 20.0000000000005 & 2.59999999999948 \tabularnewline
17 & 22.6 & 22.5998281219005 & 0.000171878099514799 \tabularnewline
18 & 22.6 & 22.5999999886377 & 1.13623386255313e-08 \tabularnewline
19 & 22.4 & 22.5999999999993 & -0.199999999999253 \tabularnewline
20 & 22.4 & 22.4000132213923 & -1.32213922690028e-05 \tabularnewline
21 & 22.4 & 22.400000000874 & -8.74024408403784e-10 \tabularnewline
22 & 18.6 & 22.4000000000001 & -3.80000000000005 \tabularnewline
23 & 18.6 & 18.6002512064531 & -0.000251206453135921 \tabularnewline
24 & 18.6 & 18.6000000166065 & -1.6606495734095e-08 \tabularnewline
25 & 16.2 & 18.6000000000011 & -2.4000000000011 \tabularnewline
26 & 16.2 & 16.2001586567072 & -0.000158656707245797 \tabularnewline
27 & 16.2 & 16.2000000104883 & -1.04883142171275e-08 \tabularnewline
28 & 13.8 & 16.2000000000007 & -2.40000000000069 \tabularnewline
29 & 13.8 & 13.8001586567072 & -0.00015865670724402 \tabularnewline
30 & 13.8 & 13.8000000104883 & -1.04883124407706e-08 \tabularnewline
31 & 24.1 & 13.8000000000007 & 10.2999999999993 \tabularnewline
32 & 24.1 & 24.0993190982981 & 0.00068090170192292 \tabularnewline
33 & 24.1 & 24.0999999549877 & 4.50123422979232e-08 \tabularnewline
34 & 19.9 & 24.099999999997 & -4.19999999999703 \tabularnewline
35 & 19.9 & 19.9002776492377 & -0.00027764923767748 \tabularnewline
36 & 19.9 & 19.9000000183545 & -1.83545481036163e-08 \tabularnewline
37 & 22.3 & 19.9000000000012 & 2.39999999999879 \tabularnewline
38 & 22.3 & 22.2998413432928 & 0.000158656707245797 \tabularnewline
39 & 22.3 & 22.2999999895117 & 1.04883142171275e-08 \tabularnewline
40 & 20.9 & 22.2999999999993 & -1.39999999999931 \tabularnewline
41 & 20.9 & 20.9000925497459 & -9.25497458936775e-05 \tabularnewline
42 & 20.9 & 20.9000000061182 & -6.11818151696752e-09 \tabularnewline
43 & 23.5 & 20.9000000000004 & 2.5999999999996 \tabularnewline
44 & 23.5 & 23.4998281219005 & 0.000171878099514799 \tabularnewline
45 & 23.5 & 23.4999999886377 & 1.13623386255313e-08 \tabularnewline
46 & 23.1 & 23.4999999999993 & -0.399999999999249 \tabularnewline
47 & 23.1 & 23.1000264427845 & -2.64427845415582e-05 \tabularnewline
48 & 23.1 & 23.1000000017481 & -1.74805236952125e-09 \tabularnewline
49 & 25.7 & 23.1000000000001 & 2.59999999999988 \tabularnewline
50 & 25.7 & 25.6998281219005 & 0.000171878099514799 \tabularnewline
51 & 25.7 & 25.6999999886377 & 1.13623386255313e-08 \tabularnewline
52 & 19.7 & 25.6999999999992 & -5.99999999999925 \tabularnewline
53 & 19.7 & 19.7003966417681 & -0.000396641768112715 \tabularnewline
54 & 19.7 & 19.7000000262208 & -2.6220781990105e-08 \tabularnewline
55 & 23.1 & 19.7000000000017 & 3.39999999999827 \tabularnewline
56 & 23.1 & 23.0997752363314 & 0.000224763668597916 \tabularnewline
57 & 23.1 & 23.0999999851416 & 1.48584433645738e-08 \tabularnewline
58 & 20.7 & 23.099999999999 & -2.39999999999902 \tabularnewline
59 & 20.7 & 20.7001586567072 & -0.000158656707245797 \tabularnewline
60 & 20.7 & 20.7000000104883 & -1.04883142171275e-08 \tabularnewline
61 & 18 & 20.7000000000007 & -2.70000000000069 \tabularnewline
62 & 18 & 18.0001784887957 & -0.000178488795651077 \tabularnewline
63 & 18 & 18.0000000117994 & -1.17993508297332e-08 \tabularnewline
64 & 16.9 & 18.0000000000008 & -1.10000000000078 \tabularnewline
65 & 16.9 & 16.9000727176575 & -7.2717657488397e-05 \tabularnewline
66 & 16.9 & 16.9000000048071 & -4.80714490436185e-09 \tabularnewline
67 & 24.4 & 16.9000000000003 & 7.49999999999968 \tabularnewline
68 & 24.4 & 24.3995041977899 & 0.000495802210139118 \tabularnewline
69 & 24.4 & 24.399999967224 & 3.27759792639881e-08 \tabularnewline
70 & 15.5 & 24.3999999999978 & -8.89999999999783 \tabularnewline
71 & 15.5 & 15.500588351956 & -0.000588351956031019 \tabularnewline
72 & 15.5 & 15.5000000388942 & -3.88941607809556e-08 \tabularnewline
73 & 18.4 & 15.5000000000026 & 2.89999999999743 \tabularnewline
74 & 18.4 & 18.3998082898121 & 0.00019171018792008 \tabularnewline
75 & 18.4 & 18.3999999873266 & 1.26733787908506e-08 \tabularnewline
76 & 16.2 & 18.3999999999992 & -2.19999999999916 \tabularnewline
77 & 16.2 & 16.200145435315 & -0.000145435314973241 \tabularnewline
78 & 16.2 & 16.2000000096143 & -9.61428625601002e-09 \tabularnewline
79 & 20.6 & 16.2000000000006 & 4.39999999999937 \tabularnewline
80 & 20.6 & 20.5997091293701 & 0.000290870629950035 \tabularnewline
81 & 20.6 & 20.5999999807714 & 1.922857251202e-08 \tabularnewline
82 & 19.8 & 20.5999999999987 & -0.799999999998729 \tabularnewline
83 & 19.8 & 19.8000528855691 & -5.28855690831165e-05 \tabularnewline
84 & 19.8 & 19.8000000034961 & -3.49610473904249e-09 \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=232209&T=2

[TABLE]
[ROW][C]Interpolation Forecasts of Exponential Smoothing[/C][/ROW]
[ROW][C]t[/C][C]Observed[/C][C]Fitted[/C][C]Residuals[/C][/ROW]
[ROW][C]2[/C][C]19.4[/C][C]19.4[/C][C]0[/C][/ROW]
[ROW][C]3[/C][C]19.4[/C][C]19.4[/C][C]0[/C][/ROW]
[ROW][C]4[/C][C]19.5[/C][C]19.4[/C][C]0.100000000000001[/C][/ROW]
[ROW][C]5[/C][C]19.5[/C][C]19.4999933893039[/C][C]6.61069613627774e-06[/C][/ROW]
[ROW][C]6[/C][C]19.5[/C][C]19.499999999563[/C][C]4.37012204201892e-10[/C][/ROW]
[ROW][C]7[/C][C]28.7[/C][C]19.5[/C][C]9.20000000000003[/C][/ROW]
[ROW][C]8[/C][C]28.7[/C][C]28.6993918159556[/C][C]0.000608184044438076[/C][/ROW]
[ROW][C]9[/C][C]28.7[/C][C]28.6999999597948[/C][C]4.02051973935613e-08[/C][/ROW]
[ROW][C]10[/C][C]21.8[/C][C]28.6999999999973[/C][C]-6.89999999999734[/C][/ROW]
[ROW][C]11[/C][C]21.8[/C][C]21.8004561380333[/C][C]-0.000456138033328557[/C][/ROW]
[ROW][C]12[/C][C]21.8[/C][C]21.8000000301539[/C][C]-3.01538989333494e-08[/C][/ROW]
[ROW][C]13[/C][C]20[/C][C]21.800000000002[/C][C]-1.80000000000199[/C][/ROW]
[ROW][C]14[/C][C]20[/C][C]20.0001189925304[/C][C]-0.000118992530435236[/C][/ROW]
[ROW][C]15[/C][C]20[/C][C]20.0000000078662[/C][C]-7.86623388648877e-09[/C][/ROW]
[ROW][C]16[/C][C]22.6[/C][C]20.0000000000005[/C][C]2.59999999999948[/C][/ROW]
[ROW][C]17[/C][C]22.6[/C][C]22.5998281219005[/C][C]0.000171878099514799[/C][/ROW]
[ROW][C]18[/C][C]22.6[/C][C]22.5999999886377[/C][C]1.13623386255313e-08[/C][/ROW]
[ROW][C]19[/C][C]22.4[/C][C]22.5999999999993[/C][C]-0.199999999999253[/C][/ROW]
[ROW][C]20[/C][C]22.4[/C][C]22.4000132213923[/C][C]-1.32213922690028e-05[/C][/ROW]
[ROW][C]21[/C][C]22.4[/C][C]22.400000000874[/C][C]-8.74024408403784e-10[/C][/ROW]
[ROW][C]22[/C][C]18.6[/C][C]22.4000000000001[/C][C]-3.80000000000005[/C][/ROW]
[ROW][C]23[/C][C]18.6[/C][C]18.6002512064531[/C][C]-0.000251206453135921[/C][/ROW]
[ROW][C]24[/C][C]18.6[/C][C]18.6000000166065[/C][C]-1.6606495734095e-08[/C][/ROW]
[ROW][C]25[/C][C]16.2[/C][C]18.6000000000011[/C][C]-2.4000000000011[/C][/ROW]
[ROW][C]26[/C][C]16.2[/C][C]16.2001586567072[/C][C]-0.000158656707245797[/C][/ROW]
[ROW][C]27[/C][C]16.2[/C][C]16.2000000104883[/C][C]-1.04883142171275e-08[/C][/ROW]
[ROW][C]28[/C][C]13.8[/C][C]16.2000000000007[/C][C]-2.40000000000069[/C][/ROW]
[ROW][C]29[/C][C]13.8[/C][C]13.8001586567072[/C][C]-0.00015865670724402[/C][/ROW]
[ROW][C]30[/C][C]13.8[/C][C]13.8000000104883[/C][C]-1.04883124407706e-08[/C][/ROW]
[ROW][C]31[/C][C]24.1[/C][C]13.8000000000007[/C][C]10.2999999999993[/C][/ROW]
[ROW][C]32[/C][C]24.1[/C][C]24.0993190982981[/C][C]0.00068090170192292[/C][/ROW]
[ROW][C]33[/C][C]24.1[/C][C]24.0999999549877[/C][C]4.50123422979232e-08[/C][/ROW]
[ROW][C]34[/C][C]19.9[/C][C]24.099999999997[/C][C]-4.19999999999703[/C][/ROW]
[ROW][C]35[/C][C]19.9[/C][C]19.9002776492377[/C][C]-0.00027764923767748[/C][/ROW]
[ROW][C]36[/C][C]19.9[/C][C]19.9000000183545[/C][C]-1.83545481036163e-08[/C][/ROW]
[ROW][C]37[/C][C]22.3[/C][C]19.9000000000012[/C][C]2.39999999999879[/C][/ROW]
[ROW][C]38[/C][C]22.3[/C][C]22.2998413432928[/C][C]0.000158656707245797[/C][/ROW]
[ROW][C]39[/C][C]22.3[/C][C]22.2999999895117[/C][C]1.04883142171275e-08[/C][/ROW]
[ROW][C]40[/C][C]20.9[/C][C]22.2999999999993[/C][C]-1.39999999999931[/C][/ROW]
[ROW][C]41[/C][C]20.9[/C][C]20.9000925497459[/C][C]-9.25497458936775e-05[/C][/ROW]
[ROW][C]42[/C][C]20.9[/C][C]20.9000000061182[/C][C]-6.11818151696752e-09[/C][/ROW]
[ROW][C]43[/C][C]23.5[/C][C]20.9000000000004[/C][C]2.5999999999996[/C][/ROW]
[ROW][C]44[/C][C]23.5[/C][C]23.4998281219005[/C][C]0.000171878099514799[/C][/ROW]
[ROW][C]45[/C][C]23.5[/C][C]23.4999999886377[/C][C]1.13623386255313e-08[/C][/ROW]
[ROW][C]46[/C][C]23.1[/C][C]23.4999999999993[/C][C]-0.399999999999249[/C][/ROW]
[ROW][C]47[/C][C]23.1[/C][C]23.1000264427845[/C][C]-2.64427845415582e-05[/C][/ROW]
[ROW][C]48[/C][C]23.1[/C][C]23.1000000017481[/C][C]-1.74805236952125e-09[/C][/ROW]
[ROW][C]49[/C][C]25.7[/C][C]23.1000000000001[/C][C]2.59999999999988[/C][/ROW]
[ROW][C]50[/C][C]25.7[/C][C]25.6998281219005[/C][C]0.000171878099514799[/C][/ROW]
[ROW][C]51[/C][C]25.7[/C][C]25.6999999886377[/C][C]1.13623386255313e-08[/C][/ROW]
[ROW][C]52[/C][C]19.7[/C][C]25.6999999999992[/C][C]-5.99999999999925[/C][/ROW]
[ROW][C]53[/C][C]19.7[/C][C]19.7003966417681[/C][C]-0.000396641768112715[/C][/ROW]
[ROW][C]54[/C][C]19.7[/C][C]19.7000000262208[/C][C]-2.6220781990105e-08[/C][/ROW]
[ROW][C]55[/C][C]23.1[/C][C]19.7000000000017[/C][C]3.39999999999827[/C][/ROW]
[ROW][C]56[/C][C]23.1[/C][C]23.0997752363314[/C][C]0.000224763668597916[/C][/ROW]
[ROW][C]57[/C][C]23.1[/C][C]23.0999999851416[/C][C]1.48584433645738e-08[/C][/ROW]
[ROW][C]58[/C][C]20.7[/C][C]23.099999999999[/C][C]-2.39999999999902[/C][/ROW]
[ROW][C]59[/C][C]20.7[/C][C]20.7001586567072[/C][C]-0.000158656707245797[/C][/ROW]
[ROW][C]60[/C][C]20.7[/C][C]20.7000000104883[/C][C]-1.04883142171275e-08[/C][/ROW]
[ROW][C]61[/C][C]18[/C][C]20.7000000000007[/C][C]-2.70000000000069[/C][/ROW]
[ROW][C]62[/C][C]18[/C][C]18.0001784887957[/C][C]-0.000178488795651077[/C][/ROW]
[ROW][C]63[/C][C]18[/C][C]18.0000000117994[/C][C]-1.17993508297332e-08[/C][/ROW]
[ROW][C]64[/C][C]16.9[/C][C]18.0000000000008[/C][C]-1.10000000000078[/C][/ROW]
[ROW][C]65[/C][C]16.9[/C][C]16.9000727176575[/C][C]-7.2717657488397e-05[/C][/ROW]
[ROW][C]66[/C][C]16.9[/C][C]16.9000000048071[/C][C]-4.80714490436185e-09[/C][/ROW]
[ROW][C]67[/C][C]24.4[/C][C]16.9000000000003[/C][C]7.49999999999968[/C][/ROW]
[ROW][C]68[/C][C]24.4[/C][C]24.3995041977899[/C][C]0.000495802210139118[/C][/ROW]
[ROW][C]69[/C][C]24.4[/C][C]24.399999967224[/C][C]3.27759792639881e-08[/C][/ROW]
[ROW][C]70[/C][C]15.5[/C][C]24.3999999999978[/C][C]-8.89999999999783[/C][/ROW]
[ROW][C]71[/C][C]15.5[/C][C]15.500588351956[/C][C]-0.000588351956031019[/C][/ROW]
[ROW][C]72[/C][C]15.5[/C][C]15.5000000388942[/C][C]-3.88941607809556e-08[/C][/ROW]
[ROW][C]73[/C][C]18.4[/C][C]15.5000000000026[/C][C]2.89999999999743[/C][/ROW]
[ROW][C]74[/C][C]18.4[/C][C]18.3998082898121[/C][C]0.00019171018792008[/C][/ROW]
[ROW][C]75[/C][C]18.4[/C][C]18.3999999873266[/C][C]1.26733787908506e-08[/C][/ROW]
[ROW][C]76[/C][C]16.2[/C][C]18.3999999999992[/C][C]-2.19999999999916[/C][/ROW]
[ROW][C]77[/C][C]16.2[/C][C]16.200145435315[/C][C]-0.000145435314973241[/C][/ROW]
[ROW][C]78[/C][C]16.2[/C][C]16.2000000096143[/C][C]-9.61428625601002e-09[/C][/ROW]
[ROW][C]79[/C][C]20.6[/C][C]16.2000000000006[/C][C]4.39999999999937[/C][/ROW]
[ROW][C]80[/C][C]20.6[/C][C]20.5997091293701[/C][C]0.000290870629950035[/C][/ROW]
[ROW][C]81[/C][C]20.6[/C][C]20.5999999807714[/C][C]1.922857251202e-08[/C][/ROW]
[ROW][C]82[/C][C]19.8[/C][C]20.5999999999987[/C][C]-0.799999999998729[/C][/ROW]
[ROW][C]83[/C][C]19.8[/C][C]19.8000528855691[/C][C]-5.28855690831165e-05[/C][/ROW]
[ROW][C]84[/C][C]19.8[/C][C]19.8000000034961[/C][C]-3.49610473904249e-09[/C][/ROW]
[/TABLE]
Source: https://freestatistics.org/blog/index.php?pk=232209&T=2

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=232209&T=2

As an alternative you can also use a QR Code:

The GUIDs for individual cells are displayed in the table below:

Interpolation Forecasts of Exponential Smoothing
t	Observed	Fitted	Residuals
2	19.4	19.4	0
3	19.4	19.4	0
4	19.5	19.4	0.100000000000001
5	19.5	19.4999933893039	6.61069613627774e-06
6	19.5	19.499999999563	4.37012204201892e-10
7	28.7	19.5	9.20000000000003
8	28.7	28.6993918159556	0.000608184044438076
9	28.7	28.6999999597948	4.02051973935613e-08
10	21.8	28.6999999999973	-6.89999999999734
11	21.8	21.8004561380333	-0.000456138033328557
12	21.8	21.8000000301539	-3.01538989333494e-08
13	20	21.800000000002	-1.80000000000199
14	20	20.0001189925304	-0.000118992530435236
15	20	20.0000000078662	-7.86623388648877e-09
16	22.6	20.0000000000005	2.59999999999948
17	22.6	22.5998281219005	0.000171878099514799
18	22.6	22.5999999886377	1.13623386255313e-08
19	22.4	22.5999999999993	-0.199999999999253
20	22.4	22.4000132213923	-1.32213922690028e-05
21	22.4	22.400000000874	-8.74024408403784e-10
22	18.6	22.4000000000001	-3.80000000000005
23	18.6	18.6002512064531	-0.000251206453135921
24	18.6	18.6000000166065	-1.6606495734095e-08
25	16.2	18.6000000000011	-2.4000000000011
26	16.2	16.2001586567072	-0.000158656707245797
27	16.2	16.2000000104883	-1.04883142171275e-08
28	13.8	16.2000000000007	-2.40000000000069
29	13.8	13.8001586567072	-0.00015865670724402
30	13.8	13.8000000104883	-1.04883124407706e-08
31	24.1	13.8000000000007	10.2999999999993
32	24.1	24.0993190982981	0.00068090170192292
33	24.1	24.0999999549877	4.50123422979232e-08
34	19.9	24.099999999997	-4.19999999999703
35	19.9	19.9002776492377	-0.00027764923767748
36	19.9	19.9000000183545	-1.83545481036163e-08
37	22.3	19.9000000000012	2.39999999999879
38	22.3	22.2998413432928	0.000158656707245797
39	22.3	22.2999999895117	1.04883142171275e-08
40	20.9	22.2999999999993	-1.39999999999931
41	20.9	20.9000925497459	-9.25497458936775e-05
42	20.9	20.9000000061182	-6.11818151696752e-09
43	23.5	20.9000000000004	2.5999999999996
44	23.5	23.4998281219005	0.000171878099514799
45	23.5	23.4999999886377	1.13623386255313e-08
46	23.1	23.4999999999993	-0.399999999999249
47	23.1	23.1000264427845	-2.64427845415582e-05
48	23.1	23.1000000017481	-1.74805236952125e-09
49	25.7	23.1000000000001	2.59999999999988
50	25.7	25.6998281219005	0.000171878099514799
51	25.7	25.6999999886377	1.13623386255313e-08
52	19.7	25.6999999999992	-5.99999999999925
53	19.7	19.7003966417681	-0.000396641768112715
54	19.7	19.7000000262208	-2.6220781990105e-08
55	23.1	19.7000000000017	3.39999999999827
56	23.1	23.0997752363314	0.000224763668597916
57	23.1	23.0999999851416	1.48584433645738e-08
58	20.7	23.099999999999	-2.39999999999902
59	20.7	20.7001586567072	-0.000158656707245797
60	20.7	20.7000000104883	-1.04883142171275e-08
61	18	20.7000000000007	-2.70000000000069
62	18	18.0001784887957	-0.000178488795651077
63	18	18.0000000117994	-1.17993508297332e-08
64	16.9	18.0000000000008	-1.10000000000078
65	16.9	16.9000727176575	-7.2717657488397e-05
66	16.9	16.9000000048071	-4.80714490436185e-09
67	24.4	16.9000000000003	7.49999999999968
68	24.4	24.3995041977899	0.000495802210139118
69	24.4	24.399999967224	3.27759792639881e-08
70	15.5	24.3999999999978	-8.89999999999783
71	15.5	15.500588351956	-0.000588351956031019
72	15.5	15.5000000388942	-3.88941607809556e-08
73	18.4	15.5000000000026	2.89999999999743
74	18.4	18.3998082898121	0.00019171018792008
75	18.4	18.3999999873266	1.26733787908506e-08
76	16.2	18.3999999999992	-2.19999999999916
77	16.2	16.200145435315	-0.000145435314973241
78	16.2	16.2000000096143	-9.61428625601002e-09
79	20.6	16.2000000000006	4.39999999999937
80	20.6	20.5997091293701	0.000290870629950035
81	20.6	20.5999999807714	1.922857251202e-08
82	19.8	20.5999999999987	-0.799999999998729
83	19.8	19.8000528855691	-5.28855690831165e-05
84	19.8	19.8000000034961	-3.49610473904249e-09

Extrapolation Forecasts of Exponential Smoothing
t	Forecast	95% Lower Bound	95% Upper Bound
85	19.8000000000002	14.7521329248574	24.847867075143
86	19.8000000000002	12.6614738783113	26.9385261216892
87	19.8000000000002	11.0572230743456	28.5427769256549
88	19.8000000000002	9.70476639430867	29.8952336056918
89	19.8000000000002	8.51322301384477	31.0867769861557
90	19.8000000000002	7.43598253329738	32.1640174667031
91	19.8000000000002	6.44535582283633	33.1546441771641
92	19.8000000000002	5.52330170241118	34.0766982975893
93	19.8000000000002	4.65728863571323	34.9427113642872
94	19.8000000000002	3.83819243807821	35.7618075619223
95	19.8000000000002	3.05912505794432	36.5408749420561
96	19.8000000000002	2.31473514620748	37.285264853793

\begin{tabular}{lllllllll}
\hline
Extrapolation Forecasts of Exponential Smoothing \tabularnewline
t & Forecast & 95% Lower Bound & 95% Upper Bound \tabularnewline
85 & 19.8000000000002 & 14.7521329248574 & 24.847867075143 \tabularnewline
86 & 19.8000000000002 & 12.6614738783113 & 26.9385261216892 \tabularnewline
87 & 19.8000000000002 & 11.0572230743456 & 28.5427769256549 \tabularnewline
88 & 19.8000000000002 & 9.70476639430867 & 29.8952336056918 \tabularnewline
89 & 19.8000000000002 & 8.51322301384477 & 31.0867769861557 \tabularnewline
90 & 19.8000000000002 & 7.43598253329738 & 32.1640174667031 \tabularnewline
91 & 19.8000000000002 & 6.44535582283633 & 33.1546441771641 \tabularnewline
92 & 19.8000000000002 & 5.52330170241118 & 34.0766982975893 \tabularnewline
93 & 19.8000000000002 & 4.65728863571323 & 34.9427113642872 \tabularnewline
94 & 19.8000000000002 & 3.83819243807821 & 35.7618075619223 \tabularnewline
95 & 19.8000000000002 & 3.05912505794432 & 36.5408749420561 \tabularnewline
96 & 19.8000000000002 & 2.31473514620748 & 37.285264853793 \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=232209&T=3

[TABLE]
[ROW][C]Extrapolation Forecasts of Exponential Smoothing[/C][/ROW]
[ROW][C]t[/C][C]Forecast[/C][C]95% Lower Bound[/C][C]95% Upper Bound[/C][/ROW]
[ROW][C]85[/C][C]19.8000000000002[/C][C]14.7521329248574[/C][C]24.847867075143[/C][/ROW]
[ROW][C]86[/C][C]19.8000000000002[/C][C]12.6614738783113[/C][C]26.9385261216892[/C][/ROW]
[ROW][C]87[/C][C]19.8000000000002[/C][C]11.0572230743456[/C][C]28.5427769256549[/C][/ROW]
[ROW][C]88[/C][C]19.8000000000002[/C][C]9.70476639430867[/C][C]29.8952336056918[/C][/ROW]
[ROW][C]89[/C][C]19.8000000000002[/C][C]8.51322301384477[/C][C]31.0867769861557[/C][/ROW]
[ROW][C]90[/C][C]19.8000000000002[/C][C]7.43598253329738[/C][C]32.1640174667031[/C][/ROW]
[ROW][C]91[/C][C]19.8000000000002[/C][C]6.44535582283633[/C][C]33.1546441771641[/C][/ROW]
[ROW][C]92[/C][C]19.8000000000002[/C][C]5.52330170241118[/C][C]34.0766982975893[/C][/ROW]
[ROW][C]93[/C][C]19.8000000000002[/C][C]4.65728863571323[/C][C]34.9427113642872[/C][/ROW]
[ROW][C]94[/C][C]19.8000000000002[/C][C]3.83819243807821[/C][C]35.7618075619223[/C][/ROW]
[ROW][C]95[/C][C]19.8000000000002[/C][C]3.05912505794432[/C][C]36.5408749420561[/C][/ROW]
[ROW][C]96[/C][C]19.8000000000002[/C][C]2.31473514620748[/C][C]37.285264853793[/C][/ROW]
[/TABLE]
Source: https://freestatistics.org/blog/index.php?pk=232209&T=3

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=232209&T=3

As an alternative you can also use a QR Code:

The GUIDs for individual cells are displayed in the table below:

Extrapolation Forecasts of Exponential Smoothing
t	Forecast	95% Lower Bound	95% Upper Bound
85	19.8000000000002	14.7521329248574	24.847867075143
86	19.8000000000002	12.6614738783113	26.9385261216892
87	19.8000000000002	11.0572230743456	28.5427769256549
88	19.8000000000002	9.70476639430867	29.8952336056918
89	19.8000000000002	8.51322301384477	31.0867769861557
90	19.8000000000002	7.43598253329738	32.1640174667031
91	19.8000000000002	6.44535582283633	33.1546441771641
92	19.8000000000002	5.52330170241118	34.0766982975893
93	19.8000000000002	4.65728863571323	34.9427113642872
94	19.8000000000002	3.83819243807821	35.7618075619223
95	19.8000000000002	3.05912505794432	36.5408749420561
96	19.8000000000002	2.31473514620748	37.285264853793

Figure 1

PNG link

Postscript link

PDF link

Figure 2

PNG link

Postscript link

PDF link

Figure 3

PNG link

Postscript link

PDF link

Parameters (Session):

par1 = 12 ; par2 = Single ; par3 = additive ;

Parameters (R input):

par1 = 12 ; par2 = Single ; par3 = additive ;

R code (references can be found in the software module):

par1 <- as.numeric(par1)
if (par2 == 'Single') K <- 1
if (par2 == 'Double') K <- 2
if (par2 == 'Triple') K <- par1
nx <- length(x)
nxmK <- nx - K
x <- ts(x, frequency = par1)
if (par2 == 'Single') fit <- HoltWinters(x, gamma=F, beta=F)
if (par2 == 'Double') fit <- HoltWinters(x, gamma=F)
if (par2 == 'Triple') fit <- HoltWinters(x, seasonal=par3)
fit
myresid <- x - fit$fitted[,'xhat']
bitmap(file='test1.png')
op <- par(mfrow=c(2,1))
plot(fit,ylab='Observed (black) / Fitted (red)',main='Interpolation Fit of Exponential Smoothing')
plot(myresid,ylab='Residuals',main='Interpolation Prediction Errors')
par(op)
dev.off()
bitmap(file='test2.png')
p <- predict(fit, par1, prediction.interval=TRUE)
np <- length(p[,1])
plot(fit,p,ylab='Observed (black) / Fitted (red)',main='Extrapolation Fit of Exponential Smoothing')
dev.off()
bitmap(file='test3.png')
op <- par(mfrow = c(2,2))
acf(as.numeric(myresid),lag.max = nx/2,main='Residual ACF')
spectrum(myresid,main='Residals Periodogram')
cpgram(myresid,main='Residal Cumulative Periodogram')
qqnorm(myresid,main='Residual Normal QQ Plot')
qqline(myresid)
par(op)
dev.off()
load(file='createtable')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a,'Estimated Parameters of Exponential Smoothing',2,TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'Parameter',header=TRUE)
a<-table.element(a,'Value',header=TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'alpha',header=TRUE)
a<-table.element(a,fit$alpha)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'beta',header=TRUE)
a<-table.element(a,fit$beta)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'gamma',header=TRUE)
a<-table.element(a,fit$gamma)
a<-table.row.end(a)
a<-table.end(a)
table.save(a,file='mytable.tab')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a,'Interpolation Forecasts of Exponential Smoothing',4,TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'t',header=TRUE)
a<-table.element(a,'Observed',header=TRUE)
a<-table.element(a,'Fitted',header=TRUE)
a<-table.element(a,'Residuals',header=TRUE)
a<-table.row.end(a)
for (i in 1:nxmK) {
a<-table.row.start(a)
a<-table.element(a,i+K,header=TRUE)
a<-table.element(a,x[i+K])
a<-table.element(a,fit$fitted[i,'xhat'])
a<-table.element(a,myresid[i])
a<-table.row.end(a)
}
a<-table.end(a)
table.save(a,file='mytable1.tab')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a,'Extrapolation Forecasts of Exponential Smoothing',4,TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'t',header=TRUE)
a<-table.element(a,'Forecast',header=TRUE)
a<-table.element(a,'95% Lower Bound',header=TRUE)
a<-table.element(a,'95% Upper Bound',header=TRUE)
a<-table.row.end(a)
for (i in 1:np) {
a<-table.row.start(a)
a<-table.element(a,nx+i,header=TRUE)
a<-table.element(a,p[i,'fit'])
a<-table.element(a,p[i,'lwr'])
a<-table.element(a,p[i,'upr'])
a<-table.row.end(a)
}
a<-table.end(a)
table.save(a,file='mytable2.tab')

Free Statistics

Description of Statistical Computation

Tree of Dependent Computations

Dataset

Tables (Output of Computation)

Figures (Output of Computation)

Input Parameters & R Code