FreeStatistics.org

Free Statistics

of Irreproducible Research!

Description of Statistical Computation

Author's title

Author*The author of this computation has been verified*
R Software Modulerwasp_smp.wasp
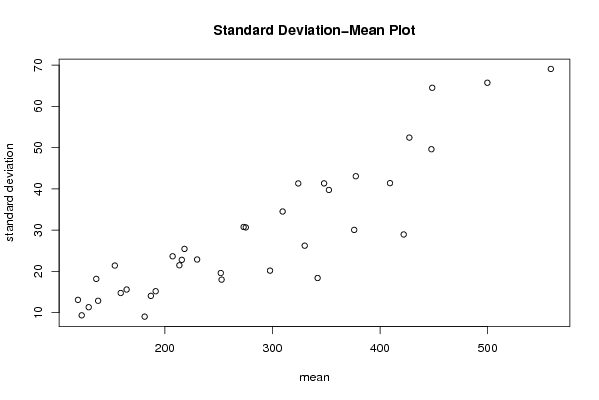
Title produced by softwareStandard Deviation-Mean Plot
Date of computationSat, 29 Nov 2008 09:26:32 -0700
Cite this page as followsStatistical Computations at FreeStatistics.org, Office for Research Development and Education, URL https://freestatistics.org/blog/index.php?v=date/2008/Nov/29/t1227977810hbdw82o1uw8wyba.htm/, Retrieved Tue, 12 Nov 2024 22:23:34 +0000
Statistical Computations at FreeStatistics.org, Office for Research Development and Education, URL https://freestatistics.org/blog/index.php?pk=26337, Retrieved Tue, 12 Nov 2024 22:23:34 +0000
QR Codes:

Original text written by user:
IsPrivate?No (this computation is public)
User-defined keywords
Estimated Impact266

Tree of Dependent Computations

Family? (F = Feedback message, R = changed R code, M = changed R Module, P = changed Parameters, D = changed Data)
F     [Univariate Data Series] [Airline data] [2007-10-18 09:58:47] [42daae401fd3def69a25014f2252b4c2]
F RMPD    [Standard Deviation-Mean Plot] [Q5 Standard DMP] [2008-11-29 16:26:32] [8a1195ff8db4df756ce44b463a631c76] [Current]
-   PD      [Standard Deviation-Mean Plot] [Q8 SDMN bouwprod] [2008-11-30 00:14:02] [aa5573c1db401b164e448aef050955a1]
- RM          [Variance Reduction Matrix] [Q8 RVM bouwprod] [2008-11-30 00:21:08] [aa5573c1db401b164e448aef050955a1]
-    D          [Variance Reduction Matrix] [Q8 VRM tot prod] [2008-11-30 00:41:13] [aa5573c1db401b164e448aef050955a1]
-    D        [Standard Deviation-Mean Plot] [Q8 SDMP tot prod] [2008-11-30 00:28:07] [aa5573c1db401b164e448aef050955a1]
-             [Standard Deviation-Mean Plot] [Q8 SDMN bouwprod] [2008-11-30 00:31:28] [aa5573c1db401b164e448aef050955a1]
-   P           [Standard Deviation-Mean Plot] [Standard Deviatio...] [2008-12-12 12:06:26] [aa5573c1db401b164e448aef050955a1]
-   P           [Standard Deviation-Mean Plot] [Standard Deviatio...] [2008-12-12 12:06:26] [aa5573c1db401b164e448aef050955a1]
-   P           [Standard Deviation-Mean Plot] [Standard Deviatio...] [2008-12-12 12:06:26] [aa5573c1db401b164e448aef050955a1]
- RMP             [Box-Cox Normality Plot] [Box Cox Normality...] [2008-12-12 12:35:24] [aa5573c1db401b164e448aef050955a1]
- RM              [Variance Reduction Matrix] [VRM Bouwproductie] [2008-12-12 13:22:47] [aa5573c1db401b164e448aef050955a1]
- RMP               [(Partial) Autocorrelation Function] [ACF bouwproductie...] [2008-12-12 13:31:29] [aa5573c1db401b164e448aef050955a1]
-   P                 [(Partial) Autocorrelation Function] [ACF bouwproductie...] [2008-12-12 13:45:52] [aa5573c1db401b164e448aef050955a1]
-   P                   [(Partial) Autocorrelation Function] [ACF bouwproductie...] [2008-12-12 13:59:06] [aa5573c1db401b164e448aef050955a1]
- RM              [Spectral Analysis] [Spectral Analysis...] [2008-12-12 14:26:07] [aa5573c1db401b164e448aef050955a1]
- RM              [Spectral Analysis] [Spectral Analysis...] [2008-12-12 14:42:38] [aa5573c1db401b164e448aef050955a1]
-    D            [Standard Deviation-Mean Plot] [SDMP Totale Produ...] [2008-12-12 15:57:50] [aa5573c1db401b164e448aef050955a1]
- RM                [Variance Reduction Matrix] [VRM Totale Productie] [2008-12-12 16:00:44] [aa5573c1db401b164e448aef050955a1]
- RMPD              [Cross Correlation Function] [CCF Bouwproductie...] [2008-12-12 16:06:05] [aa5573c1db401b164e448aef050955a1]
-   P                 [Cross Correlation Function] [CCF Bouwproductie...] [2008-12-12 16:12:34] [aa5573c1db401b164e448aef050955a1]
-           [Standard Deviation-Mean Plot] [Verbetering Q6 - ...] [2008-12-05 18:25:02] [57850c80fd59ccfb28f882be994e814e]
-           [Standard Deviation-Mean Plot] [Q5] [2008-12-08 11:56:13] [b85eb1eb4b13b870c6e7ebbba3e34fcc]
-   P       [Standard Deviation-Mean Plot] [Correctie Q5] [2008-12-08 20:38:30] [aa5573c1db401b164e448aef050955a1]
Feedback Forum
2008-12-06 09:08:42 [Siem Van Opstal] [reply] 
correcte conclusie

Post a new message

Dataset

Dataseries X:
Download CSV
Histogram
Boxplots 
112
118
132
129
121
135
148
148
136
119
104
118
115
126
141
135
125
149
170
170
158
133
114
140
145
150
178
163
172
178
199
199
184
162
146
166
171
180
193
181
183
218
230
242
209
191
172
194
196
196
236
235
229
243
264
272
237
211
180
201
204
188
235
227
234
264
302
293
259
229
203
229
242
233
267
269
270
315
364
347
312
274
237
278
284
277
317
313
318
374
413
405
355
306
271
306
315
301
356
348
355
422
465
467
404
347
305
336
340
318
362
348
363
435
491
505
404
359
310
337
360
342
406
396
420
472
548
559
463
407
362
405
417
391
419
461
472
535
622
606
508
461
390
432

Tables (Output of Computation)





Summary of computational transaction
Raw Inputview raw input (R code)
Raw Outputview raw output of R engine
Computing time1 seconds
R Server'Gwilym Jenkins' @ 72.249.127.135

\begin{tabular}{lllllllll}
\hline
Summary of computational transaction \tabularnewline
Raw Input & view raw input (R code)  \tabularnewline
Raw Output & view raw output of R engine  \tabularnewline
Computing time & 1 seconds \tabularnewline
R Server & 'Gwilym Jenkins' @ 72.249.127.135 \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=26337&T=0

[TABLE]
[ROW][C]Summary of computational transaction[/C][/ROW]
[ROW][C]Raw Input[/C][C]view raw input (R code) [/C][/ROW]
[ROW][C]Raw Output[/C][C]view raw output of R engine [/C][/ROW]
[ROW][C]Computing time[/C][C]1 seconds[/C][/ROW]
[ROW][C]R Server[/C][C]'Gwilym Jenkins' @ 72.249.127.135[/C][/ROW]
[/TABLE]
Source: https://freestatistics.org/blog/index.php?pk=26337&T=0

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=26337&T=0

As an alternative you can also use a QR Code:  
QR Code


The GUIDs for individual cells are displayed in the table below:

Summary of computational transaction
Raw Inputview raw input (R code)
Raw Outputview raw output of R engine
Computing time1 seconds
R Server'Gwilym Jenkins' @ 72.249.127.135






Standard Deviation-Mean Plot
SectionMeanStandard DeviationRange
1122.759.3585967609109720
213812.884098726725127
3119.2513.098982148752432
4129.2511.324751652906126
5153.521.424285285628545
6136.2518.191115047370444
715914.764823060233433
818714.071247279470327
9164.515.609825965290838
10181.259.0323492698928222
11218.2525.460754112948059
12191.515.198684153570737
13215.7522.808989455914140
1425219.612920911140943
15207.2523.669600757089257
16213.521.486429825977847
17273.2530.782841540919168
1823022.891046284519256
19252.7518.006943105369136
2032441.336021417967594
21275.2530.674364975768775
22297.7520.188693205191240
23377.543.0851869362795
24309.534.530180036213784
2533026.242459234352855
26427.2552.4491817540242112
2734841.352146256270799
2834218.402898322456344
29448.564.5264803523845142
30352.539.753406562624794
3137630.066592756745864
32499.7565.7488909919146139
33409.2541.4115523334572101
3442228.959742171964670
35558.7569.0959477827752150
36447.7549.6277811983033118

\begin{tabular}{lllllllll}
\hline
Standard Deviation-Mean Plot \tabularnewline
Section & Mean & Standard Deviation & Range \tabularnewline
1 & 122.75 & 9.35859676091097 & 20 \tabularnewline
2 & 138 & 12.8840987267251 & 27 \tabularnewline
3 & 119.25 & 13.0989821487524 & 32 \tabularnewline
4 & 129.25 & 11.3247516529061 & 26 \tabularnewline
5 & 153.5 & 21.4242852856285 & 45 \tabularnewline
6 & 136.25 & 18.1911150473704 & 44 \tabularnewline
7 & 159 & 14.7648230602334 & 33 \tabularnewline
8 & 187 & 14.0712472794703 & 27 \tabularnewline
9 & 164.5 & 15.6098259652908 & 38 \tabularnewline
10 & 181.25 & 9.03234926989282 & 22 \tabularnewline
11 & 218.25 & 25.4607541129480 & 59 \tabularnewline
12 & 191.5 & 15.1986841535707 & 37 \tabularnewline
13 & 215.75 & 22.8089894559141 & 40 \tabularnewline
14 & 252 & 19.6129209111409 & 43 \tabularnewline
15 & 207.25 & 23.6696007570892 & 57 \tabularnewline
16 & 213.5 & 21.4864298259778 & 47 \tabularnewline
17 & 273.25 & 30.7828415409191 & 68 \tabularnewline
18 & 230 & 22.8910462845192 & 56 \tabularnewline
19 & 252.75 & 18.0069431053691 & 36 \tabularnewline
20 & 324 & 41.3360214179675 & 94 \tabularnewline
21 & 275.25 & 30.6743649757687 & 75 \tabularnewline
22 & 297.75 & 20.1886932051912 & 40 \tabularnewline
23 & 377.5 & 43.08518693627 & 95 \tabularnewline
24 & 309.5 & 34.5301800362137 & 84 \tabularnewline
25 & 330 & 26.2424592343528 & 55 \tabularnewline
26 & 427.25 & 52.4491817540242 & 112 \tabularnewline
27 & 348 & 41.3521462562707 & 99 \tabularnewline
28 & 342 & 18.4028983224563 & 44 \tabularnewline
29 & 448.5 & 64.5264803523845 & 142 \tabularnewline
30 & 352.5 & 39.7534065626247 & 94 \tabularnewline
31 & 376 & 30.0665927567458 & 64 \tabularnewline
32 & 499.75 & 65.7488909919146 & 139 \tabularnewline
33 & 409.25 & 41.4115523334572 & 101 \tabularnewline
34 & 422 & 28.9597421719646 & 70 \tabularnewline
35 & 558.75 & 69.0959477827752 & 150 \tabularnewline
36 & 447.75 & 49.6277811983033 & 118 \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=26337&T=1

[TABLE]
[ROW][C]Standard Deviation-Mean Plot[/C][/ROW]
[ROW][C]Section[/C][C]Mean[/C][C]Standard Deviation[/C][C]Range[/C][/ROW]
[ROW][C]1[/C][C]122.75[/C][C]9.35859676091097[/C][C]20[/C][/ROW]
[ROW][C]2[/C][C]138[/C][C]12.8840987267251[/C][C]27[/C][/ROW]
[ROW][C]3[/C][C]119.25[/C][C]13.0989821487524[/C][C]32[/C][/ROW]
[ROW][C]4[/C][C]129.25[/C][C]11.3247516529061[/C][C]26[/C][/ROW]
[ROW][C]5[/C][C]153.5[/C][C]21.4242852856285[/C][C]45[/C][/ROW]
[ROW][C]6[/C][C]136.25[/C][C]18.1911150473704[/C][C]44[/C][/ROW]
[ROW][C]7[/C][C]159[/C][C]14.7648230602334[/C][C]33[/C][/ROW]
[ROW][C]8[/C][C]187[/C][C]14.0712472794703[/C][C]27[/C][/ROW]
[ROW][C]9[/C][C]164.5[/C][C]15.6098259652908[/C][C]38[/C][/ROW]
[ROW][C]10[/C][C]181.25[/C][C]9.03234926989282[/C][C]22[/C][/ROW]
[ROW][C]11[/C][C]218.25[/C][C]25.4607541129480[/C][C]59[/C][/ROW]
[ROW][C]12[/C][C]191.5[/C][C]15.1986841535707[/C][C]37[/C][/ROW]
[ROW][C]13[/C][C]215.75[/C][C]22.8089894559141[/C][C]40[/C][/ROW]
[ROW][C]14[/C][C]252[/C][C]19.6129209111409[/C][C]43[/C][/ROW]
[ROW][C]15[/C][C]207.25[/C][C]23.6696007570892[/C][C]57[/C][/ROW]
[ROW][C]16[/C][C]213.5[/C][C]21.4864298259778[/C][C]47[/C][/ROW]
[ROW][C]17[/C][C]273.25[/C][C]30.7828415409191[/C][C]68[/C][/ROW]
[ROW][C]18[/C][C]230[/C][C]22.8910462845192[/C][C]56[/C][/ROW]
[ROW][C]19[/C][C]252.75[/C][C]18.0069431053691[/C][C]36[/C][/ROW]
[ROW][C]20[/C][C]324[/C][C]41.3360214179675[/C][C]94[/C][/ROW]
[ROW][C]21[/C][C]275.25[/C][C]30.6743649757687[/C][C]75[/C][/ROW]
[ROW][C]22[/C][C]297.75[/C][C]20.1886932051912[/C][C]40[/C][/ROW]
[ROW][C]23[/C][C]377.5[/C][C]43.08518693627[/C][C]95[/C][/ROW]
[ROW][C]24[/C][C]309.5[/C][C]34.5301800362137[/C][C]84[/C][/ROW]
[ROW][C]25[/C][C]330[/C][C]26.2424592343528[/C][C]55[/C][/ROW]
[ROW][C]26[/C][C]427.25[/C][C]52.4491817540242[/C][C]112[/C][/ROW]
[ROW][C]27[/C][C]348[/C][C]41.3521462562707[/C][C]99[/C][/ROW]
[ROW][C]28[/C][C]342[/C][C]18.4028983224563[/C][C]44[/C][/ROW]
[ROW][C]29[/C][C]448.5[/C][C]64.5264803523845[/C][C]142[/C][/ROW]
[ROW][C]30[/C][C]352.5[/C][C]39.7534065626247[/C][C]94[/C][/ROW]
[ROW][C]31[/C][C]376[/C][C]30.0665927567458[/C][C]64[/C][/ROW]
[ROW][C]32[/C][C]499.75[/C][C]65.7488909919146[/C][C]139[/C][/ROW]
[ROW][C]33[/C][C]409.25[/C][C]41.4115523334572[/C][C]101[/C][/ROW]
[ROW][C]34[/C][C]422[/C][C]28.9597421719646[/C][C]70[/C][/ROW]
[ROW][C]35[/C][C]558.75[/C][C]69.0959477827752[/C][C]150[/C][/ROW]
[ROW][C]36[/C][C]447.75[/C][C]49.6277811983033[/C][C]118[/C][/ROW]
[/TABLE]
Source: https://freestatistics.org/blog/index.php?pk=26337&T=1

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=26337&T=1

As an alternative you can also use a QR Code:  
QR Code


The GUIDs for individual cells are displayed in the table below:

Standard Deviation-Mean Plot
SectionMeanStandard DeviationRange
1122.759.3585967609109720
213812.884098726725127
3119.2513.098982148752432
4129.2511.324751652906126
5153.521.424285285628545
6136.2518.191115047370444
715914.764823060233433
818714.071247279470327
9164.515.609825965290838
10181.259.0323492698928222
11218.2525.460754112948059
12191.515.198684153570737
13215.7522.808989455914140
1425219.612920911140943
15207.2523.669600757089257
16213.521.486429825977847
17273.2530.782841540919168
1823022.891046284519256
19252.7518.006943105369136
2032441.336021417967594
21275.2530.674364975768775
22297.7520.188693205191240
23377.543.0851869362795
24309.534.530180036213784
2533026.242459234352855
26427.2552.4491817540242112
2734841.352146256270799
2834218.402898322456344
29448.564.5264803523845142
30352.539.753406562624794
3137630.066592756745864
32499.7565.7488909919146139
33409.2541.4115523334572101
3442228.959742171964670
35558.7569.0959477827752150
36447.7549.6277811983033118






Regression: S.E.(k) = alpha + beta * Mean(k)
alpha-5.80099763154143
beta0.123476027685633
S.D.0.0103446045667054
T-STAT11.9362733383784
p-value1.04276839477293e-13

\begin{tabular}{lllllllll}
\hline
Regression: S.E.(k) = alpha + beta * Mean(k) \tabularnewline
alpha & -5.80099763154143 \tabularnewline
beta & 0.123476027685633 \tabularnewline
S.D. & 0.0103446045667054 \tabularnewline
T-STAT & 11.9362733383784 \tabularnewline
p-value & 1.04276839477293e-13 \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=26337&T=2

[TABLE]
[ROW][C]Regression: S.E.(k) = alpha + beta * Mean(k)[/C][/ROW]
[ROW][C]alpha[/C][C]-5.80099763154143[/C][/ROW]
[ROW][C]beta[/C][C]0.123476027685633[/C][/ROW]
[ROW][C]S.D.[/C][C]0.0103446045667054[/C][/ROW]
[ROW][C]T-STAT[/C][C]11.9362733383784[/C][/ROW]
[ROW][C]p-value[/C][C]1.04276839477293e-13[/C][/ROW]
[/TABLE]
Source: https://freestatistics.org/blog/index.php?pk=26337&T=2

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=26337&T=2

As an alternative you can also use a QR Code:  
QR Code


The GUIDs for individual cells are displayed in the table below:

Regression: S.E.(k) = alpha + beta * Mean(k)
alpha-5.80099763154143
beta0.123476027685633
S.D.0.0103446045667054
T-STAT11.9362733383784
p-value1.04276839477293e-13






Regression: ln S.E.(k) = alpha + beta * ln Mean(k)
alpha-2.90863185200523
beta1.10425535603129
S.D.0.100433173418818
T-STAT10.9949264614632
p-value9.7344626745232e-13
Lambda-0.104255356031287

\begin{tabular}{lllllllll}
\hline
Regression: ln S.E.(k) = alpha + beta * ln Mean(k) \tabularnewline
alpha & -2.90863185200523 \tabularnewline
beta & 1.10425535603129 \tabularnewline
S.D. & 0.100433173418818 \tabularnewline
T-STAT & 10.9949264614632 \tabularnewline
p-value & 9.7344626745232e-13 \tabularnewline
Lambda & -0.104255356031287 \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=26337&T=3

[TABLE]
[ROW][C]Regression: ln S.E.(k) = alpha + beta * ln Mean(k)[/C][/ROW]
[ROW][C]alpha[/C][C]-2.90863185200523[/C][/ROW]
[ROW][C]beta[/C][C]1.10425535603129[/C][/ROW]
[ROW][C]S.D.[/C][C]0.100433173418818[/C][/ROW]
[ROW][C]T-STAT[/C][C]10.9949264614632[/C][/ROW]
[ROW][C]p-value[/C][C]9.7344626745232e-13[/C][/ROW]
[ROW][C]Lambda[/C][C]-0.104255356031287[/C][/ROW]
[/TABLE]
Source: https://freestatistics.org/blog/index.php?pk=26337&T=3

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=26337&T=3

As an alternative you can also use a QR Code:  
QR Code


The GUIDs for individual cells are displayed in the table below:

Regression: ln S.E.(k) = alpha + beta * ln Mean(k)
alpha-2.90863185200523
beta1.10425535603129
S.D.0.100433173418818
T-STAT10.9949264614632
p-value9.7344626745232e-13
Lambda-0.104255356031287


Figures (Output of Computation)

Input Parameters & R Code

Parameters (Session):
par1 = 4 ;
Parameters (R input):
par1 = 4 ;
R code (references can be found in the software module):
par1 <- as.numeric(par1)
(n <- length(x))
(np <- floor(n / par1))
arr <- array(NA,dim=c(par1,np))
j <- 0
k <- 1
for (i in 1:(np*par1))
{
j = j + 1
arr[j,k] <- x[i]
if (j == par1) {
j = 0
k=k+1
}
}
arr
arr.mean <- array(NA,dim=np)
arr.sd <- array(NA,dim=np)
arr.range <- array(NA,dim=np)
for (j in 1:np)
{
arr.mean[j] <- mean(arr[,j],na.rm=TRUE)
arr.sd[j] <- sd(arr[,j],na.rm=TRUE)
arr.range[j] <- max(arr[,j],na.rm=TRUE) - min(arr[,j],na.rm=TRUE)
}
arr.mean
arr.sd
arr.range
(lm1 <- lm(arr.sd~arr.mean))
(lnlm1 <- lm(log(arr.sd)~log(arr.mean)))
(lm2 <- lm(arr.range~arr.mean))
bitmap(file='test1.png')
plot(arr.mean,arr.sd,main='Standard Deviation-Mean Plot',xlab='mean',ylab='standard deviation')
dev.off()
bitmap(file='test2.png')
plot(arr.mean,arr.range,main='Range-Mean Plot',xlab='mean',ylab='range')
dev.off()
load(file='createtable')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a,'Standard Deviation-Mean Plot',4,TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'Section',header=TRUE)
a<-table.element(a,'Mean',header=TRUE)
a<-table.element(a,'Standard Deviation',header=TRUE)
a<-table.element(a,'Range',header=TRUE)
a<-table.row.end(a)
for (j in 1:np) {
a<-table.row.start(a)
a<-table.element(a,j,header=TRUE)
a<-table.element(a,arr.mean[j])
a<-table.element(a,arr.sd[j] )
a<-table.element(a,arr.range[j] )
a<-table.row.end(a)
}
a<-table.end(a)
table.save(a,file='mytable.tab')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a,'Regression: S.E.(k) = alpha + beta * Mean(k)',2,TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'alpha',header=TRUE)
a<-table.element(a,lm1$coefficients[[1]])
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'beta',header=TRUE)
a<-table.element(a,lm1$coefficients[[2]])
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'S.D.',header=TRUE)
a<-table.element(a,summary(lm1)$coefficients[2,2])
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'T-STAT',header=TRUE)
a<-table.element(a,summary(lm1)$coefficients[2,3])
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'p-value',header=TRUE)
a<-table.element(a,summary(lm1)$coefficients[2,4])
a<-table.row.end(a)
a<-table.end(a)
table.save(a,file='mytable1.tab')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a,'Regression: ln S.E.(k) = alpha + beta * ln Mean(k)',2,TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'alpha',header=TRUE)
a<-table.element(a,lnlm1$coefficients[[1]])
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'beta',header=TRUE)
a<-table.element(a,lnlm1$coefficients[[2]])
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'S.D.',header=TRUE)
a<-table.element(a,summary(lnlm1)$coefficients[2,2])
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'T-STAT',header=TRUE)
a<-table.element(a,summary(lnlm1)$coefficients[2,3])
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'p-value',header=TRUE)
a<-table.element(a,summary(lnlm1)$coefficients[2,4])
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'Lambda',header=TRUE)
a<-table.element(a,1-lnlm1$coefficients[[2]])
a<-table.row.end(a)
a<-table.end(a)
table.save(a,file='mytable2.tab')