FreeStatistics.org

Free Statistics

of Irreproducible Research!

Description of Statistical Computation

Author's title

Author*The author of this computation has been verified*
R Software Modulerwasp_cross.wasp
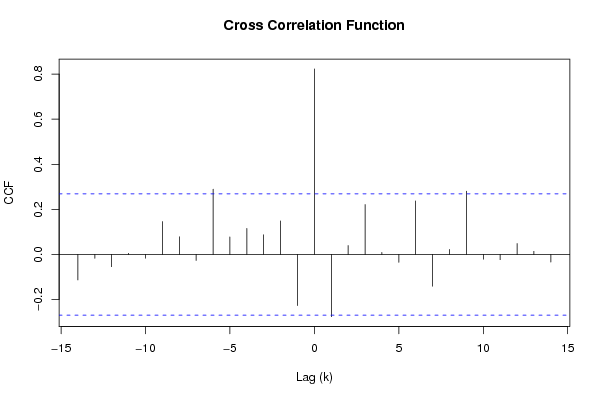
Title produced by softwareCross Correlation Function
Date of computationFri, 12 Dec 2008 09:06:05 -0700
Cite this page as followsStatistical Computations at FreeStatistics.org, Office for Research Development and Education, URL https://freestatistics.org/blog/index.php?v=date/2008/Dec/12/t1229098061nw2y8why23f8tgy.htm/, Retrieved Sun, 10 Nov 2024 19:50:18 +0000
Statistical Computations at FreeStatistics.org, Office for Research Development and Education, URL https://freestatistics.org/blog/index.php?pk=32856, Retrieved Sun, 10 Nov 2024 19:50:18 +0000
QR Codes:

Original text written by user:
IsPrivate?No (this computation is public)
User-defined keywords
Estimated Impact245

Tree of Dependent Computations

Family? (F = Feedback message, R = changed R code, M = changed R Module, P = changed Parameters, D = changed Data)
F     [Univariate Data Series] [Airline data] [2007-10-18 09:58:47] [42daae401fd3def69a25014f2252b4c2]
F RMPD  [Standard Deviation-Mean Plot] [Q5 Standard DMP] [2008-11-29 16:26:32] [aa5573c1db401b164e448aef050955a1]
-   PD    [Standard Deviation-Mean Plot] [Q8 SDMN bouwprod] [2008-11-30 00:14:02] [aa5573c1db401b164e448aef050955a1]
-           [Standard Deviation-Mean Plot] [Q8 SDMN bouwprod] [2008-11-30 00:31:28] [aa5573c1db401b164e448aef050955a1]
-   P         [Standard Deviation-Mean Plot] [Standard Deviatio...] [2008-12-12 12:06:26] [aa5573c1db401b164e448aef050955a1]
-    D          [Standard Deviation-Mean Plot] [SDMP Totale Produ...] [2008-12-12 15:57:50] [aa5573c1db401b164e448aef050955a1]
- RMPD              [Cross Correlation Function] [CCF Bouwproductie...] [2008-12-12 16:06:05] [8a1195ff8db4df756ce44b463a631c76] [Current]
-   P                 [Cross Correlation Function] [CCF Bouwproductie...] [2008-12-12 16:12:34] [aa5573c1db401b164e448aef050955a1]
Feedback Forum

Post a new message

Dataset

Dataseries X:
Download CSV
Histogram
Boxplots 
82.7
88.9
105.9
100.8
94
105
58.5
87.6
113.1
112.5
89.6
74.5
82.7
90.1
109.4
96
89.2
109.1
49.1
92.9
107.7
103.5
91.1
79.8
71.9
82.9
90.1
100.7
90.7
108.8
44.1
93.6
107.4
96.5
93.6
76.5
76.7
84
103.3
88.5
99
105.9
44.7
94
107.1
104.8
102.5
77.7
85.2
91.3
106.5
92.4
97.5
107
51.1
98.6
102.2
114.3
99.4
72.5
92.3
99.4
85.9
109.4
97.6
Dataseries Y:
Download CSV
Histogram 
97.4
97
105.4
102.7
98.1
104.5
87.4
89.9
109.8
111.7
98.6
96.9
95.1
97
112.7
102.9
97.4
111.4
87.4
96.8
114.1
110.3
103.9
101.6
94.6
95.9
104.7
102.8
98.1
113.9
80.9
95.7
113.2
105.9
108.8
102.3
99
100.7
115.5
100.7
109.9
114.6
85.4
100.5
114.8
116.5
112.9
102
106
105.3
118.8
106.1
109.3
117.2
92.5
104.2
112.5
122.4
113.3
100
110.7
112.8
109.8
117.3
109.1

Tables (Output of Computation)





Summary of computational transaction
Raw Inputview raw input (R code)
Raw Outputview raw output of R engine
Computing time1 seconds
R Server'George Udny Yule' @ 72.249.76.132

\begin{tabular}{lllllllll}
\hline
Summary of computational transaction \tabularnewline
Raw Input & view raw input (R code)  \tabularnewline
Raw Output & view raw output of R engine  \tabularnewline
Computing time & 1 seconds \tabularnewline
R Server & 'George Udny Yule' @ 72.249.76.132 \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=32856&T=0

[TABLE]
[ROW][C]Summary of computational transaction[/C][/ROW]
[ROW][C]Raw Input[/C][C]view raw input (R code) [/C][/ROW]
[ROW][C]Raw Output[/C][C]view raw output of R engine [/C][/ROW]
[ROW][C]Computing time[/C][C]1 seconds[/C][/ROW]
[ROW][C]R Server[/C][C]'George Udny Yule' @ 72.249.76.132[/C][/ROW]
[/TABLE]
Source: https://freestatistics.org/blog/index.php?pk=32856&T=0

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=32856&T=0

As an alternative you can also use a QR Code:  
QR Code


The GUIDs for individual cells are displayed in the table below:

Summary of computational transaction
Raw Inputview raw input (R code)
Raw Outputview raw output of R engine
Computing time1 seconds
R Server'George Udny Yule' @ 72.249.76.132






Cross Correlation Function
ParameterValue
Box-Cox transformation parameter (lambda) of X series1
Degree of non-seasonal differencing (d) of X series0
Degree of seasonal differencing (D) of X series1
Seasonal Period (s)12
Box-Cox transformation parameter (lambda) of Y series-0.3
Degree of non-seasonal differencing (d) of Y series0
Degree of seasonal differencing (D) of Y series1
krho(Y[t],X[t+k])
-14-0.112957144443798
-13-0.0170590793006017
-12-0.0542438938561712
-110.00501355605826753
-10-0.0167795332382039
-90.145939957259910
-80.0783396495783074
-7-0.0266367802616172
-60.289453668445007
-50.0778679995643515
-40.115141411556326
-30.087110926595982
-20.148346045491675
-1-0.226865839030919
00.822937269520483
1-0.276081869657279
20.0391110614998513
30.221150665104147
40.00902278399666934
5-0.0351876892192394
60.23724187364668
7-0.141098718222786
80.0219350059877049
90.280505564278467
10-0.0209727829025178
11-0.0230694081653727
120.0485003003362191
130.0139794066527003
14-0.0336405421345838

\begin{tabular}{lllllllll}
\hline
Cross Correlation Function \tabularnewline
Parameter & Value \tabularnewline
Box-Cox transformation parameter (lambda) of X series & 1 \tabularnewline
Degree of non-seasonal differencing (d) of X series & 0 \tabularnewline
Degree of seasonal differencing (D) of X series & 1 \tabularnewline
Seasonal Period (s) & 12 \tabularnewline
Box-Cox transformation parameter (lambda) of Y series & -0.3 \tabularnewline
Degree of non-seasonal differencing (d) of Y series & 0 \tabularnewline
Degree of seasonal differencing (D) of Y series & 1 \tabularnewline
k & rho(Y[t],X[t+k]) \tabularnewline
-14 & -0.112957144443798 \tabularnewline
-13 & -0.0170590793006017 \tabularnewline
-12 & -0.0542438938561712 \tabularnewline
-11 & 0.00501355605826753 \tabularnewline
-10 & -0.0167795332382039 \tabularnewline
-9 & 0.145939957259910 \tabularnewline
-8 & 0.0783396495783074 \tabularnewline
-7 & -0.0266367802616172 \tabularnewline
-6 & 0.289453668445007 \tabularnewline
-5 & 0.0778679995643515 \tabularnewline
-4 & 0.115141411556326 \tabularnewline
-3 & 0.087110926595982 \tabularnewline
-2 & 0.148346045491675 \tabularnewline
-1 & -0.226865839030919 \tabularnewline
0 & 0.822937269520483 \tabularnewline
1 & -0.276081869657279 \tabularnewline
2 & 0.0391110614998513 \tabularnewline
3 & 0.221150665104147 \tabularnewline
4 & 0.00902278399666934 \tabularnewline
5 & -0.0351876892192394 \tabularnewline
6 & 0.23724187364668 \tabularnewline
7 & -0.141098718222786 \tabularnewline
8 & 0.0219350059877049 \tabularnewline
9 & 0.280505564278467 \tabularnewline
10 & -0.0209727829025178 \tabularnewline
11 & -0.0230694081653727 \tabularnewline
12 & 0.0485003003362191 \tabularnewline
13 & 0.0139794066527003 \tabularnewline
14 & -0.0336405421345838 \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=32856&T=1

[TABLE]
[ROW][C]Cross Correlation Function[/C][/ROW]
[ROW][C]Parameter[/C][C]Value[/C][/ROW]
[ROW][C]Box-Cox transformation parameter (lambda) of X series[/C][C]1[/C][/ROW]
[ROW][C]Degree of non-seasonal differencing (d) of X series[/C][C]0[/C][/ROW]
[ROW][C]Degree of seasonal differencing (D) of X series[/C][C]1[/C][/ROW]
[ROW][C]Seasonal Period (s)[/C][C]12[/C][/ROW]
[ROW][C]Box-Cox transformation parameter (lambda) of Y series[/C][C]-0.3[/C][/ROW]
[ROW][C]Degree of non-seasonal differencing (d) of Y series[/C][C]0[/C][/ROW]
[ROW][C]Degree of seasonal differencing (D) of Y series[/C][C]1[/C][/ROW]
[ROW][C]k[/C][C]rho(Y[t],X[t+k])[/C][/ROW]
[ROW][C]-14[/C][C]-0.112957144443798[/C][/ROW]
[ROW][C]-13[/C][C]-0.0170590793006017[/C][/ROW]
[ROW][C]-12[/C][C]-0.0542438938561712[/C][/ROW]
[ROW][C]-11[/C][C]0.00501355605826753[/C][/ROW]
[ROW][C]-10[/C][C]-0.0167795332382039[/C][/ROW]
[ROW][C]-9[/C][C]0.145939957259910[/C][/ROW]
[ROW][C]-8[/C][C]0.0783396495783074[/C][/ROW]
[ROW][C]-7[/C][C]-0.0266367802616172[/C][/ROW]
[ROW][C]-6[/C][C]0.289453668445007[/C][/ROW]
[ROW][C]-5[/C][C]0.0778679995643515[/C][/ROW]
[ROW][C]-4[/C][C]0.115141411556326[/C][/ROW]
[ROW][C]-3[/C][C]0.087110926595982[/C][/ROW]
[ROW][C]-2[/C][C]0.148346045491675[/C][/ROW]
[ROW][C]-1[/C][C]-0.226865839030919[/C][/ROW]
[ROW][C]0[/C][C]0.822937269520483[/C][/ROW]
[ROW][C]1[/C][C]-0.276081869657279[/C][/ROW]
[ROW][C]2[/C][C]0.0391110614998513[/C][/ROW]
[ROW][C]3[/C][C]0.221150665104147[/C][/ROW]
[ROW][C]4[/C][C]0.00902278399666934[/C][/ROW]
[ROW][C]5[/C][C]-0.0351876892192394[/C][/ROW]
[ROW][C]6[/C][C]0.23724187364668[/C][/ROW]
[ROW][C]7[/C][C]-0.141098718222786[/C][/ROW]
[ROW][C]8[/C][C]0.0219350059877049[/C][/ROW]
[ROW][C]9[/C][C]0.280505564278467[/C][/ROW]
[ROW][C]10[/C][C]-0.0209727829025178[/C][/ROW]
[ROW][C]11[/C][C]-0.0230694081653727[/C][/ROW]
[ROW][C]12[/C][C]0.0485003003362191[/C][/ROW]
[ROW][C]13[/C][C]0.0139794066527003[/C][/ROW]
[ROW][C]14[/C][C]-0.0336405421345838[/C][/ROW]
[/TABLE]
Source: https://freestatistics.org/blog/index.php?pk=32856&T=1

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=32856&T=1

As an alternative you can also use a QR Code:  
QR Code


The GUIDs for individual cells are displayed in the table below:

Cross Correlation Function
ParameterValue
Box-Cox transformation parameter (lambda) of X series1
Degree of non-seasonal differencing (d) of X series0
Degree of seasonal differencing (D) of X series1
Seasonal Period (s)12
Box-Cox transformation parameter (lambda) of Y series-0.3
Degree of non-seasonal differencing (d) of Y series0
Degree of seasonal differencing (D) of Y series1
krho(Y[t],X[t+k])
-14-0.112957144443798
-13-0.0170590793006017
-12-0.0542438938561712
-110.00501355605826753
-10-0.0167795332382039
-90.145939957259910
-80.0783396495783074
-7-0.0266367802616172
-60.289453668445007
-50.0778679995643515
-40.115141411556326
-30.087110926595982
-20.148346045491675
-1-0.226865839030919
00.822937269520483
1-0.276081869657279
20.0391110614998513
30.221150665104147
40.00902278399666934
5-0.0351876892192394
60.23724187364668
7-0.141098718222786
80.0219350059877049
90.280505564278467
10-0.0209727829025178
11-0.0230694081653727
120.0485003003362191
130.0139794066527003
14-0.0336405421345838


Figures (Output of Computation)

Input Parameters & R Code

Parameters (Session):
par1 = 1 ; par2 = 0 ; par3 = 1 ; par4 = 12 ; par5 = -0.3 ; par6 = 0 ; par7 = 1 ;
Parameters (R input):
par1 = 1 ; par2 = 0 ; par3 = 1 ; par4 = 12 ; par5 = -0.3 ; par6 = 0 ; par7 = 1 ;
R code (references can be found in the software module):
par1 <- as.numeric(par1)
par2 <- as.numeric(par2)
par3 <- as.numeric(par3)
par4 <- as.numeric(par4)
par5 <- as.numeric(par5)
par6 <- as.numeric(par6)
par7 <- as.numeric(par7)
if (par1 == 0) {
x <- log(x)
} else {
x <- (x ^ par1 - 1) / par1
}
if (par5 == 0) {
y <- log(y)
} else {
y <- (y ^ par5 - 1) / par5
}
if (par2 > 0) x <- diff(x,lag=1,difference=par2)
if (par6 > 0) y <- diff(y,lag=1,difference=par6)
if (par3 > 0) x <- diff(x,lag=par4,difference=par3)
if (par7 > 0) y <- diff(y,lag=par4,difference=par7)
x
y
bitmap(file='test1.png')
(r <- ccf(x,y,main='Cross Correlation Function',ylab='CCF',xlab='Lag (k)'))
dev.off()
load(file='createtable')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a,'Cross Correlation Function',2,TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'Parameter',header=TRUE)
a<-table.element(a,'Value',header=TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'Box-Cox transformation parameter (lambda) of X series',header=TRUE)
a<-table.element(a,par1)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'Degree of non-seasonal differencing (d) of X series',header=TRUE)
a<-table.element(a,par2)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'Degree of seasonal differencing (D) of X series',header=TRUE)
a<-table.element(a,par3)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'Seasonal Period (s)',header=TRUE)
a<-table.element(a,par4)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'Box-Cox transformation parameter (lambda) of Y series',header=TRUE)
a<-table.element(a,par5)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'Degree of non-seasonal differencing (d) of Y series',header=TRUE)
a<-table.element(a,par6)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'Degree of seasonal differencing (D) of Y series',header=TRUE)
a<-table.element(a,par7)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'k',header=TRUE)
a<-table.element(a,'rho(Y[t],X[t+k])',header=TRUE)
a<-table.row.end(a)
mylength <- length(r$acf)
myhalf <- floor((mylength-1)/2)
for (i in 1:mylength) {
a<-table.row.start(a)
a<-table.element(a,i-myhalf-1,header=TRUE)
a<-table.element(a,r$acf[i])
a<-table.row.end(a)
}
a<-table.end(a)
table.save(a,file='mytable.tab')